Vertical tangent

In mathematics, particularly calculus, a vertical tangent is tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency.
Limit definition
A function ƒ has a vertical tangent at x = a if the difference quotient used to define the derivative has infinite limit:
The first case corresponds to an upward-sloping vertical tangent, and the second case to a downward-sloping vertical tangent. Informally speaking, the graph of ƒ has a vertical tangent at x = a if the derivative of ƒ at a is either positive or negative infinity.
For a continuous function, it is often possible to detect a vertical tangent by taking the limit of the derivative. If
then ƒ must have an upward-sloping vertical tangent at x = a. Similarly, if
then ƒ must have a downward-sloping vertical tangent at x = a. In these situations, the vertical tangent to ƒ appears as a vertical asymptote on the graph of the derivative.
Vertical cusps
Closely related to vertical tangents are vertical cusps. This occurs when the one-sided derivatives are both infinite, but one is positive and the other is negative. For example, if
then the graph of ƒ will have a vertical cusp that slopes up on the left side and down on the right side.
As with vertical tangents, vertical cusps can sometimes be detected for a continuous function by examining the limit of the derivative. For example, if
then the graph of ƒ will have a vertical cusp that slopes down on the left side and up on the right side. This corresponds to a vertical asymptote on the graph of the derivative that goes to 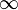 on the left and
on the left and 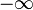 on the right.
on the right.
Example
The function
has a vertical tangent at x = 0, since it is continuous and
Similarly, the function
has a vertical cusp at x = 0, since it is continuous,
and
References
Vertical Tangents and Cusps. Retrieved May 12, 2006.
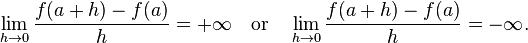
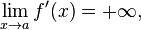
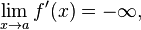
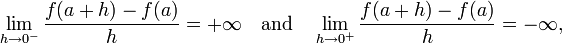
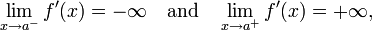
![f(x) = \sqrt[3]{x}](../I/m/b592d4981e272d6edd9ec4263a0a874b.png)
![\lim_{x\to 0} f'(x) \;=\; \lim_{x\to 0} \frac{1}{\sqrt[3]{x^2}} \;=\; \infty.](../I/m/59e9536196b212751f909d7a35eb8e51.png)
![g(x) = \sqrt[3]{x^2}](../I/m/288b0e22c451d3a71ac4674d668800c7.png)
![\lim_{x\to 0^-} g'(x) \;=\; \lim_{x\to 0^-} \frac{1}{\sqrt[3]{x}} \;=\; {-\infty}\text{,}](../I/m/5502442358ed5a9e259a6197dd4b9942.png)
![\lim_{x\to 0^+} g'(x) \;=\; \lim_{x\to 0^+} \frac{1}{\sqrt[3]{x}} \;=\; {+\infty}\text{.}](../I/m/8d037b7f193c58da7770039cbc18932d.png)