UCERF3
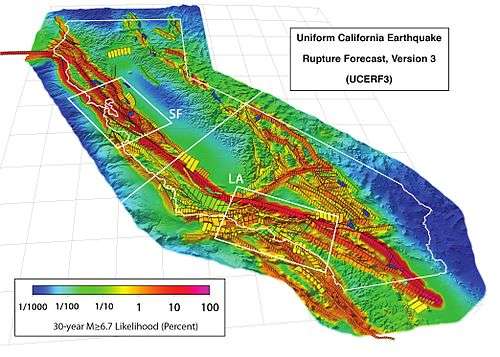
The 2015 Uniform California Earthquake Rupture Forecast, Version 3, or UCERF3, is the latest official earthquake rupture forecast (ERF) for the state of California, superseding UCERF2. It provides authoritative estimates of the likelihood and severity of potentially damaging earthquake ruptures in the long- and near-term. Combining this with ground motion models produces estimates of the severity of ground shaking that can be expected during a given period (seismic hazard), and of the threat to the built environment (seismic risk). This information is used to inform engineering design and building codes, planning for disaster, and evaluating whether earthquake insurance premiums are sufficient for the prospective losses.[1] A variety of hazard metrics [2] can be calculated with UCERF3; a typical metric is the likelihood of a magnitude[3] M 6.7 earthquake (the size of the 1994 Northridge earthquake) in the 30 years (typical life of a mortgage) since 2014.
UCERF3 was prepared by the Working Group on California Earthquake Probabilities (WGCEP), a collaboration between the United States Geological Survey (USGS), the California Geological Survey (CGS), and the Southern California Earthquake Center (SCEC), with significant funding from the California Earthquake Authority (CEA).[4]
Highlights
A major achievement of UCERF3 is use of a new methodology that can model multifault ruptures such as have been observed in recent earthquakes.[5] This allows seismicity to be distributed in a more realistic manner, which has corrected a problem with prior studies that overpredicted earthquakes of moderate size (between magnitude 6.5 and 7.0).[6] The rate of earthquakes of magnitude (M[7]) 6.7 and greater (over the entire state) is now believed to be about one in 6.3 years, instead of one in 4.8 years. On the other hand, earthquakes of magnitude 8 and larger are now expected about every 494 years (down from 617).[8] Otherwise the overall expectations of seismicity are generally in line with earlier results.[9] (See Table A for a summary of the overall rates.)
The fault model database has been revised and expanded to cover over 350 fault sections, up from about 200 for UCERF2, and new attributes added to better characterize the faults.[10] Various technical improvements have also been made.[11]
Table A: Estimated probabilities (minimum, most likely, and maximum) of an earthquake of the given magnitude in the next thirty years for different regions of California1 M≥ 6.0 6.7 7.0 7.5 7.7 8.0 All CA 100% 100% 100% 97% 100% 100% 77% 93% 100% 17% 48% 85% 3% 27% 71% 0% 7% 32% N. CA 100% 100% 100% 84% 95% 100% 55% 76% 96% 8% 28% 60% 1% 15% 45% 0% 5% 25% S. CA 100% 100% 100% 77% 93% 100% 44% 75% 97% 9% 36% 79% 2% 22% 68% 0% 7% 32% SF 89% 98% 100% 52% 72% 94% 27% 51% 84% 5% 20% 43% 0% 10% 32% 0% 4% 21% LA 84% 96% 100% 28% 60% 92% 17% 46% 87% 5% 31% 77% 1% 20% 68% 0% 7% 32% - 1. From Table 7 in Field et al. 2015, p. 529. "M" is moment magnitude (p. 512).
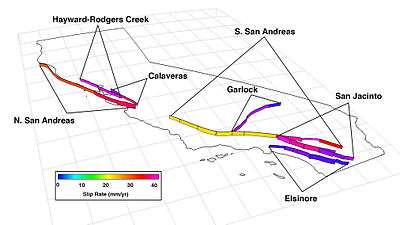
Of the six main faults evaluated in previous studies the Southern San Andreas fault remains the most likely to experience an M ≥ 6.7 earthquake in the next 30 years. The largest increase in such liklihood is on the Calaveras fault (see main faults map for location), where the mean (most likely) value is now set at 25%. The old value, of 8%, is less than the minimum now expected (10%). The previous under-estimate is believed to be due mostly to not modeling multifault ruptures, which limited the size of many ruptures.[13]
The largest probability decrease is on the San Jacinto fault, which went from 32% to 9%. Again this is due to multifault rupturing, but here the effect is fewer earthquakes, but they are more likely to be bigger (M ≥ 7.7) [14]
Table B
Table B: Aggregate probabilities of an M ≥ 6.7 earthquake within 30 years (and change from UCERF2)1 Fault2 Section maps3 QFFDB
fault#4Length5 Notable Earthquakes Min.6 Mean Max. San Andreas Fault south Parkfield
Cholame
Carrizo
Big Bend
Mojave N
Mojave S
San Bernardino N
San Bernardino S
San Gorgonio Pass
N. Branch Mill Cr
Coachella546 km
339 miles17%
(-6%)53%
(-7%)93%
(-1%)San Andreas Fault north Offshore
North Coast
Peninsula
Santa Cruz Mts
Creeping Section472 km
293 miles1%
(-5%)33%
(+12%)73%
(+33%)Hayward/
Rodgers Creek Fault150 km
93 miles14%
(-2%)32%
(0%)54%
(-14%)Calaveras Fault 123 km
76 miles1911 Calaveras earthquake [15]
1979 Coyote Lake earthquake [16]
1984 Morgan Hill earthquake [17]
2007 Alum Rock earthquake [18]10%
(+8%)25%
(+17%)54%
(+32%)San Jacinto Fault Zone San Bernardino
San Jacinto Valley
Stepovers
Anza
Clark
Coyote Creek
Borrego
Superstition Mtn309 km
192 miles0%
(-14%)9%
(23%)35%
(-20%)Garlock Fault 254 km
158 miles0%
(-3%)8%
(+2%)37%
(+24%)Elsinore Fault Zone Whittier
Glen Ivy
Stepovers
Temecula
Julian
Coyote Mountains249 km
217 miles1910 Elsinore earthquake
1%
(-4%)5%
(-6%)17%
(-8%)- Notes.
- 1. Adapted from Table 6 in Field et al. 2015, p. 525. Values are aggregated from the fault sections comprising each fault. Some sections have higher individual probabilities; see Table 4 in Field et al. 2015, p. 523. "M" is moment magnitude (p. 512).
- 2. These are the six faults for which UCERF2 had enough data to do stress-renewal modeling. The Hayward fault zone and Rodgers Creek fault are treated as a single fault; the San Andreas fault is treated as two sections.
- 3. UCEF3 fault sections, with links to "participation" maps for each section (outlined in black), showing the rate (in color) that section participates in ruptures with other sections. Participation maps for all fault sections available at http://pubs.usgs.gov/of/2013/1165/data/UCERF3_SupplementalFiles/UCERF3.3/Model/FaultParticipation/ Some faults have had sections added or split since UCERF2.
- 4. USGS Quaternary Fault and Fold Database fault numbers, with links to summary reports. QFFDB maps are no longer available.
- 5. Lengths from UCERF-2, Table 4; may vary from QFFDB values.
- 6. Min. and Max. probabilities correspond to the least and most likely alternatives in the logic tree; the Mean is a weighted average.
- 7. Slip-rates not included due to variation across sections and deformation models. See figure C21 (below) for an illustration.
Methodology
California earthquakes result from the Pacific Plate, heading approximately northwest, sliding past the North American continent. This requires accommodation of 34 to 48 millimeters (about one and a half inches) of slippage per year,[19] with some of that taken up in portions of the Basin and Range Province to the east of California.[20] This slippage is accommodated by ruptures (earthquakes) and aseismic creep on the various faults, with the frequency of ruptures dependent (in part) on how the slippage is distributed across the various faults.
Modeling
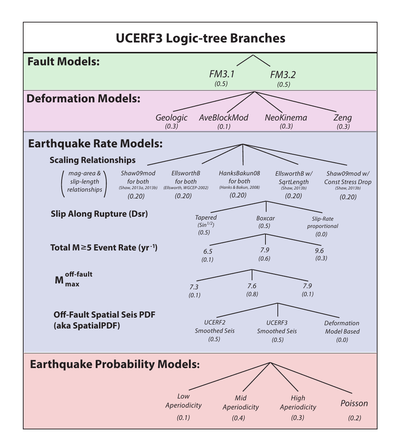
Like its predecessor, UCERF3 determines this based on four layers of modeling:[22]
- The fault models (FM 3.1 and 3.2) describe the physical geometry of the larger and more active faults.
- Deformation models determine the slip rates and related factors for each fault section, how much strain accumulates before a fault ruptures, and how much energy is then released. Four deformation models are used, reflecting different approaches to handling earthquake dynamics.
- The earthquake rate model (ERM) fits together all this data to estimate the long-term rate of rupturing.
- The probability model estimates how close (ready) each fault segment is to rupturing given how much stress has accumulated since its last rupture.
The first three layers of modeling are used to determine the long-term, or Time Independent, estimates of the magnitude, location, and frequency of potentially damaging earthquakes in California. The Time Dependent model is based on the theory of elastic rebound, that after an earthquake releases tectonic stress there will be some time before sufficient stress accumulates to cause another earthquake. In theory, this should produce some regularity in the earthquakes on a given fault, and knowing the date of the last rupture is a clue to how soon the next one can be expected. In practice this is not so clear, in part because slip rates vary, and also because fault segments influence each other, so a rupture on one segment triggers rupturing on adjacent segments. One of the achievements of UCERF3 is to better handle such multifault ruptures.[23]
The various alternatives (see diagram), taken in different combinations, form a logic tree of 1440 branches for the Time Independent model, and, when the four probability models are factored in, 5760 branches for the Time Dependent model. Each branch was evaluated and weighted according to its relative probability and importance. The UCERF3 results are an average of all these weighted alternatives.[24]
"The Grand Inversion"
In UCERF2 each fault was modeled separately,[25] as if ruptures do not extend to other faults. This assumption of fault segmentation was suspected as the cause of UCERF2 predicting nearly twice as many earthquakes in the M 6.5 to 7.0 range then actually observed, and is contrary to the multifault rupturing seen in many earthquakes.[26]
UCERF3 subdivides each fault section (as modeled by the Fault Models) into subsections (2606 segments for FM 3.1, and 2665 for FM 3.2), then considers ruptures of multiple segments regardless of which parent fault they belong to. After removing those ruptures considered implausible there are 253,706 possibilities to consider for FM 3.1, and 305,709 for FM 3.2. This compares to less than 8,000 ruptures considered in UCERF2, and reflects the high connectivity of California's fault system.[27]

A significant achievement of UCERF is development of system-level approach called the "grand inversion".[29] This uses a supercomputer to solve a system of linear equations that simultaneously satisfies multiple constraints such as known slip rates, etc.[30] The result is a model (set of values) that best fits the available data. In balancing these various factors it also provides an estimate of how much seismicity is not accounted for in the fault model, possibly in faults not yet discovered. The amount of slip occurring on unidentified faults has been estimated at between 5 and about 20 mm/yr depending on the location (generally higher in the LA area) and deformation model, with one model reaching 30 mm/yr just north of LA.[31]
Assessment
While UCERF3 represents a considerable improvement over UCERF2,[32] and the best available science to-date for estimating Cailfornia's earthquake hazard,[33] the authors caution that it remains an approximation of the natural system.[34] There are a number of assumptions in the Time Independent model,[35] while the final (Time Dependent) model explicitly "assumes elastic rebound dominates other known and suspected processes that are not included in the model."[36] Among the known processes not included is spatiotemporal clustering .[37]
There are a number of sources of uncertainty, such as insufficient knowledge of fault geometry (especially at depth) and slip rates,[38] and there is considerable challenge in how to balance the various elements of the model to achieve the best fit with the available observations. For example, there is difficulty fitting paleoseismic data and slip rates on the southern San Andreas Fault, resulting in estimates of seismicity that run about 25% less than seen in the paleoseismic data. The data does fit if a certain constraint (the regional Magnitude-Frequency Distribution) is relaxed, but this brings back the problem over-predicting moderate events.[39]
An important result is that the generally accepted Gutenberg-Richter (GR) relationship (that the distribution of earthquakes shows a certain relationship between magnitude and frequency) is inconsistent with certain parts of the current UCERF3 model. The model implies that achieving GR consistency would require certain changes in seismological understanding that "fall outside the current bounds of consensus-level acceptability".[40] Whether the Gutenberg-Richter relation is inapplicable at the scale of individual faults, or some basis of the model is incorrect, "will be equally profound scientifically, and quite consequential with respect to hazard."[41]
See also
Notes
- ↑ Field et al. 2013, p. 2.
- ↑ For a list of evaluation metrics available as of 2013 see Table 11 in Field et al. 2013, p. 52.
- ↑ Following standard seismological practice, all earthquake magnitudes here are per the moment magnitude scale. This is generally equivalent to the better known Richter magnitude scale.
- ↑ Field et al. 2013, p. 2.
- ↑ Field et al. 2015, p. 512.
- ↑ Field 2015, pp. 2–3.
- ↑ Unless otherwise noted, all earthquake magnitudes herein are according to the moment magnitude scale, per Field et al. 2015, p. 512.
- ↑ Field 2015.
- ↑ Field 2015.
- ↑ Field et al. 2013, pp. xiii, 11.
- ↑ Field et al. 2013.
- ↑ Figure 4 in Field et al. 2015, p. 520.
- ↑ Field et al. 2015, pp. 525–526; Field 2015.
- ↑ Field et al. 2015, pp. 525–526; Field.
- ↑ Dozer et al. 2009, pp. 1746–1759
- ↑ Yeats 2012, p. 92
- ↑ Hartzell & Heaton 1986, p. 649
- ↑ Oppenheimer et al. 2010
- ↑ Parsons et al. 2013, p. 57, Table C7.
- ↑ Parsons et al. 2013, p. 54.
- ↑ Figure 3 from Field et al. 2015, p. 514.
- ↑ Field et al. 2013, p. 5.
- ↑ Field et al. 2015, p. 513.
- ↑ Field et al. 2015, p. 521.
- ↑ Field et al. 2013, p. 27.
- ↑ Field et al. 2013, p. 3; Field 2015, p. 2.
- ↑ Field et al. 2013, pp. 27–28, 51.
- ↑ Parsons et al. 2013
- ↑ Field 2015, p. 5; Field et al. 2013, pp. 3, 27–28. See Page et al. 2014 for details.
- ↑ Field et al. 2013, p. 51.
- ↑ Page et al. 2014, pp. 44–45, Fig. C16.
- ↑ Field et al. 2013, p. 90.
- ↑ Field et al. 2015, p. 541.
- ↑ Field et al. 2015, pp. 512, 539. In an earlier report Field et al. (2013, p. 7) call it a "crude approximation".
- ↑ See Table 16 in Field et al. 2013, p. 89, which lists 15 key assumptions.
- ↑ Field et al. 2015, p. 541.
- ↑ Field et al. 2015, p. 512.
- ↑ Field et al. 2013, p. 87.
- ↑ Field et al. 2013, pp. 88–89. Discussion at pp 55-56.
- ↑ Field et al. 2013, pp. 86–87. Specifically, GR consistency seems to require one or more of the following: "(1) a higher degree of creep both on and off faults; (2) higher long-term rate of earthquakes over the whole region (and significant temporal variability on faults such as the SAF); (3) more fault connectivity throughout the state (for example, ~M8 anywhere); and (or) (4) lower shear rigidity."
- ↑ Field et al. 2013, p. 87.
Sources
- Dozer, D. I.; Olsen, K. B.; Pollitz, F. F.; Stein, R. S.; Toda, S. (2009), "The 1911 M∼6.6 Calaveras Earthquake: Source Parameters and the Role of Static, Viscoelastic, and Dynamic Coulomb Stress Changes Imparted by the 1906 San Francisco Earthquake", Bulletin of the Seismological Society of America, 99 (3): 1746–1759, doi:10.1785/0120080305.
- Field, Edward H.; Biasi, Glenn P.; Bird, Peter; Dawson, Timothy E.; Felzer, Karen R.; Jackson, David D.; Johnson, Kaj M.; Jordan, Thomas H.; Madden, Christopher; Michael, Andrew J.; Milner, Kevin R.; Page, Morgan T.; Parsons, Tom; Powers, Peter M.; Shaw, Bruce E.; Thatcher, Wayne R.; Weldon, Ray J., II; Zeng, Yuehua (2013), "Uniform California earthquake rupture forecast, version 3 (UCERF3) -- The time-independent model", U.S. Geological Survey, Open-File Report 2013–1165. Also California Geological Survey Special Report 228, and Southern California Earthquake Center Publication 1792. Also published in the BSSA as Field et al. 2014.
- Field, Edward H.; Arrowsmith, Ramon J.; Biasi, Glenn P.; Bird, Peter; Dawson, Timothy E.; Felzer, Karen R.; Jackson, David D.; Johnson, Kaj M.; Jordan, Thomas H.; Madden, Christopher; Michael, Andrew J.; Milner, Kevin R.; Page, Morgan T.; Parsons, Tom; Powers, Peter M.; Shaw, Bruce E.; Thatcher, Wayne R.; Weldon, Ray J., II; Zeng, Yuehua (June 2014), "Uniform California Earthquake Rupture Forecast, Version 3 (UCERF3) – The Time-Independent Model" (PDF), Bulletin of the Seismological Society of America, 104 (3): 1122–1180, doi:10.1785/0120140093.
- Field, Edward H.; et al. (WGCEP) (March 2015), "UCERF3: A New Earthquake Forecast for California's Complex Fault System" (PDF), U.S. Geological Survey, Fact Sheet 2015-3009, doi:10.3133/fs20153009, ISSN 2327-6932.
- Field, Edward H.; Biasi, Glenn P.; Bird, Peter; Dawson, Timothy E.; Felzer, Karen R.; Jackson, David D.; Johnson, Kaj M.; Jordan, Thomas H.; Madden, Christopher; Michael, Andrew J.; Milner, Kevin R.; Page, Morgan T.; Parsons, Tom; Powers, Peter M.; Shaw, Bruce E.; Thatcher, Wayne R.; Weldon, Ray J., II; Zeng, Yuehua (April 2015), "Long-Term Time-Dependent Probabilities for the Third Uniform California Earthquake Rupture Forecast (UCERF3)" (PDF), Bulletin of the Seismological Society of America, 105 (2A): 511–543, doi:10.1785/0120140093.
- Hartzell, S. H.; Heaton, T. H. (1986), "Rupture history of the 1984 Morgan Hill, California, earthquake from the inversion of strong ground records" (PDF), Bulletin of the Seismological Society of America, 76 (3): 649.
- Oppenheimer, D. H.; Bakun, W. H.; Parsons, T.; Simpson, R. W.; Boatwright, J. B.; Uhrhammer, R. A. (2010), "The 2007 M5.4 Alum Rock, California, earthquake: Implications for future earthquakes on the central and southern Calaveras Fault", Journal of Geophysical Research, 115 (B8), doi:10.1029/2009jb006683.
- Page, Morgan T.; Field, Edward H.; Milner, Kevin R.; Powers, Peter M. (June 2014), "The UCERF3 Grand Inversion: Solving for the Long-Term Rate of Ruptures in a Fault System" (PDF), Bulletin of the Seismological Society of America, 104 (3): 1181–1204, doi:10.1785/0120130180.
- Parsons, Tom; Johnson, Kaj M.; Bird, Peter; Bormann, Jayne; Dawson, Timothy E.; Field, Edward H.; Hammond, William C.; Herring, Thomas A.; McCaffrey, Rob; Shen, Zhen-Kang; Thatcher, Wayne R.; Weldon II, Ray J.; Zeng, Yuehua (2013), "Appendix C - Deformation Models for UCERF3", U.S. Geological Survey, Open-File Report 2013–1165.
External links
- USGS Fact Sheet on UCERF3
- Working Group on California Earthquake Probabilities (WGCEP)
- UCER3 website (WGCEP)
- USGS Open-File Report 2013–1165, with appendices and supplemental material.
- U.S. Geological Survey (USGS)
- California Geological Survey (CGS)
- Southern California Earthquake Center (SCEC)
- CGS Fault Activity Map
- Recent earthquakes in Calif. and Nevada (SCEC)
- Can earthquakes be predicted? (USGS) A good explanation.
- Recent earthquakes in the U.S. (USGS)
- National Seismic Hazard Maps and related resources (USGS)
- Quaternary Fault and Fold Database(USGS)