Delta-ring
In mathematics, a nonempty collection of sets  is called a δ-ring (pronounced delta-ring) if it is closed under union, relative complementation, and countable intersection:
is called a δ-ring (pronounced delta-ring) if it is closed under union, relative complementation, and countable intersection:
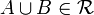 if
if 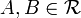
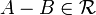 if
if 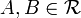
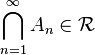 if
if 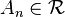 for all
for all 
If only the first two properties are satisfied, then  is a ring but not a δ-ring. Every σ-ring is a δ-ring, but not every δ-ring is a σ-ring.
is a ring but not a δ-ring. Every σ-ring is a δ-ring, but not every δ-ring is a σ-ring.
δ-rings can be used instead of σ-fields in the development of measure theory if one does not wish to allow sets of infinite measure.
See also
References
- Cortzen, Allan. "Delta-Ring." From MathWorld—A Wolfram Web Resource, created by Eric W. Weisstein. http://mathworld.wolfram.com/Delta-Ring.html
This article is issued from Wikipedia - version of the 3/16/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.