Parsec

Parsec
A parsec is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond (the diagram is not to scale).
Unit information
Unit system	astronomical units
Unit of	length
Symbol	pc
Unit conversions
1 pc in ...	... is equal to ...
metric (SI) units	3.0857×10^16 m
imperial & US units	1.9174×10^13 mi
astronomical units	2.0626×10^5 au    3.26156 ly

A parsec (symbol: pc) is a unit of length used to measure large distances to objects outside our Solar System. One parsec is the distance at which one astronomical unit subtends an angle of one arcsecond.^[1] A parsec is equal to about 3.26 light-years (31 trillion kilometres or 19 trillion miles) in length. The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun.^[2] Most of the stars visible to the unaided eye in the nighttime sky are within 500 parsecs of the Sun.

The parsec unit was likely first suggested in 1913 by the British astronomer Herbert Hall Turner.^[3] Named from an abbreviation of the parallax of one arcsecond, it was defined so as to make calculations of astronomical distances quick and easy for astronomers from only their raw observational data. Partly for this reason, it is still the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and everyday usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for all but the closest galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.

In August 2015, the IAU passed Resolution B2, which as part of the definition of a standardized absolute and apparent bolometric magnitude scale, included an explicit definition of the parsec as exactly 648000/π astronomical units, or approximately 3.08567758149137×10¹⁶ metres (based on the IAU 2012 exact SI definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many contemporary astronomical references.^[4][5]

History and derivation

The parsec is defined as being equal to the length of the longer leg of an extremely elongated imaginary right triangle in space. The two dimensions on which this triangle is based are its shorter leg, of length one astronomical unit (the average Earth-Sun distance), and the subtended angle of the vertex opposite that leg, measuring one arcsecond. Applying the rules of trigonometry to these two values, the unit length of the other leg of the triangle (the parsec) can be derived.

One of the oldest methods used by astronomers to calculate the distance to a star was to record the difference in angle between two measurements of the position of the star in the sky. The first measurement was taken from the Earth on one side of the Sun, and the second was taken half a year later, when the Earth was on the opposite side of the Sun. The distance between the two positions of the Earth when the two measurements were taken was known to be twice the distance between the Earth and the Sun. The difference in angle between the two measurements was known to be twice the parallax angle, which is formed by lines from the Sun and Earth to the star at the distant vertex. Then the distance to the star could be calculated using trigonometry.^[6] The first successful published direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the 3.5-parsec distance of 61 Cygni.^[7]

stellar parallax motion from annual parallax

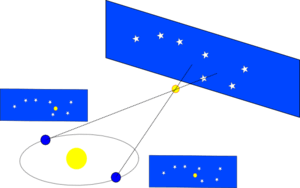
The parallax of a star is taken to be half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. Equivalently, it is the subtended angle, from that star's perspective, of the semimajor axis of the Earth's orbit. The star, the Sun and the Earth form the corners of an imaginary right triangle in space: the right angle is the corner at the Sun, and the corner at the star is the parallax angle. The length of the opposite side to the parallax angle is the distance from the Earth to the Sun (defined as one astronomical unit (au), and the length of the adjacent side gives the distance from the sun to the star. Therefore, given a measurement of the parallax angle, along with the rules of trigonometry, the distance from the Sun to the star can be found. A parsec is defined as the length of the side adjacent to the vertex occupied by a star whose parallax angle is one arcsecond.

The use of the parsec as a unit of distance follows naturally from Bessel's method, because the distance in parsecs can be computed simply as the reciprocal of the parallax angle in arcseconds (i.e. if the parallax angle is 1 arcsecond, the object is 1 pc from the Sun; if the parallax angle is 0.5 arcseconds, the object is 2 pc away; etc.). No trigonometric functions are required in this relationship because the very small angles involved mean that the approximate solution of the skinny triangle can be applied.

Though it may have been used before, the term parsec was first mentioned in an astronomical publication in 1913. Astronomer Royal Frank Watson Dyson expressed his concern for the need of a name for that unit of distance. He proposed the name astron, but mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec.^[3] It was Turner's proposal that stuck.

Calculating the value of a parsec

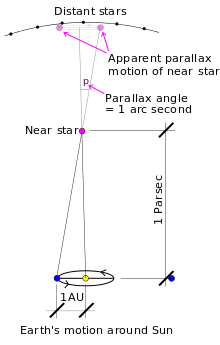
In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (au). The angle SDE is one arcsecond (1/3600 of a degree) so by definition D is a point in space at a distance of one parsec from the Sun. Through trigonometry, the distance SD is calculated as follows:

${\displaystyle \mathrm {SD} ={\frac {\mathrm {ES} }{\tan 1''}}}$

Using the small-angle approximation,^{[lower-alpha 1]} by which the tangent of an extremely small angle is almost equal to the angle itself (in radians),

${\displaystyle \mathrm {SD} \approx {\frac {\mathrm {ES} }{1''}}={\frac {1\,{\mbox{au}}}{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,{\mbox{au}}\approx 206\,264.81{\mbox{ au}}.}$

Because the astronomical unit is defined to be 149597870700 m,^[8] the following can be calculated:

π/3 pc = 60³ au = 216000 × 149597870700 m = 32313140071200 km (exactly)

Therefore, 1 parsec	≈ 206264.81 astronomical units
	≈ 3.0856776×10^16 metres
	≈ 19.173512 trillion miles
	≈ 3.2615638 light-years

A corollary states that a parsec is also the distance from which a disc one astronomical unit in diameter must be viewed for it to have an angular diameter of one arcsecond (by placing the observer at D and a diameter of the disc on ES).

The length of the parsec adopted in IAU 2015 Resolution B2^[9] (exactly 648000/π astronomical units) corresponds exactly to that derived using the small-angle calculation. This differs from the classic inverse-tangent definition by about 200 km, i.e. only after the 11th significant figure. As the astronomical unit was defined by the IAU (2012) as an exact SI length in metres, so now the parsec corresponds to an exact SI length in metres.

Usage and measurement

The parallax method is the fundamental calibration step for distance determination in astrophysics; however, the accuracy of ground-based telescope measurements of parallax angle is limited to about 0.01 arcseconds, and thus to stars no more than 100 pc distant.^[10] This is because the Earth's atmosphere limits the sharpness of a star's image.^[11] Space-based telescopes are not limited by this effect and can accurately measure distances to objects beyond the limit of ground-based observations. Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for about 100000 stars with an astrometric precision of about 0.97 milliarcseconds, and obtained accurate measurements for stellar distances of stars up to 1000 pc away.^[12][13]

ESA's Gaia satellite, which launched on 19 December 2013, is intended to measure one billion stellar distances to within 20 microarcseconds, producing errors of 10% in measurements as far as the Galactic Centre, about 8000 pc away in the constellation of Sagittarius.^[14]

Distances in parsecs

Distances less than a parsec

Distances expressed in fractions of a parsec usually involve objects within a single star system. So, for example:

• One astronomical unit (au), the distance from the Sun to the Earth, is just under 5×10⁻⁶ parsecs.
• The most distant space probe, Voyager 1, was 0.00066 parsecs from Earth as of August 2016. It took Voyager 1 39 years to cover that distance.
• The Oort cloud is estimated to be approximately 0.6 parsecs in diameter

The jet erupting from the active galactic nucleus of M87 is thought to be 1.5 kiloparsecs (4890 ly) long. (image from Hubble Space Telescope)

Parsecs and kiloparsecs

Distances expressed in parsecs (pc) include distances between nearby stars, such as those in the same spiral arm or globular cluster. A distance of 1000 parsecs (3262 light-years) is commonly denoted by the kiloparsec (kpc). Astronomers typically use kiloparsecs to express distances between parts of a galaxy, or within groups of galaxies. So, for example:

• One parsec is approximately 3.26 light-years.
• The nearest known star to the Earth, other than the Sun, Proxima Centauri, is about 1.30 parsecs (4.24 light-years) away, by direct parallax measurement.
• The distance to the open cluster Pleiades is 130±10 pc (420±32.6 ly) from us, per Hipparcos parallax measurement.
• The centre of the Milky Way is more than 8 kiloparsecs (26000 ly) from the Earth, and the Milky Way is roughly 34 kpc (110000 ly) across.
• The Andromeda Galaxy (M31) is about 780 kpc (2.5 million light-years) away from the Earth.

Megaparsecs and gigaparsecs

A distance of one million parsecs is commonly denoted by the megaparsec (Mpc). Astronomers typically express the distances between neighbouring galaxies and galaxy clusters in megaparsecs.

Galactic distances are sometimes given in units of Mpc/h (as in "50/h Mpc", also written "50 Mpc h⁻¹"). h is a parameter in the range 0.5 < h < 0.75 reflecting the uncertainty in the value of the Hubble constant H for the rate of expansion of the universe: h = H/100 km/s/Mpc. The Hubble constant becomes relevant when converting an observed redshift z into a distance d using the formula d ≈ c/H × z.^[15]

One gigaparsec (Gpc) is one billion parsecs — one of the largest units of length commonly used. One gigaparsec is about 3.26 billion light-years, or roughly 1/14 of the distance to the horizon of the observable universe (dictated by the cosmic background radiation). Astronomers typically use gigaparsecs to express the sizes of large-scale structures such as the size of, and distance to, the CfA2 Great Wall; the distances between galaxy clusters; and the distance to quasars.

For example:

• The Andromeda Galaxy is about 0.78 Mpc (2.5 million light-years) from the Earth.
• The nearest large galaxy cluster, the Virgo Cluster, is about 16.5 Mpc (54 million light-years) from the Earth.^[16]
• The galaxy RXJ1242-11, observed to have a supermassive black hole core similar to the Milky Way's, is about 200 Mpc (650 million light-years) from the Earth.
• The galaxy filament Hercules–Corona Borealis Great Wall, currently the largest known structure in the universe, is about 3 Gpc (10 billion light-years) across.
• The particle horizon (the boundary of the observable universe) has a radius of about 14.0 Gpc (46 billion light-years).^[17]

Volume units

To determine the number of stars in the Milky Way, volumes in cubic kiloparsecs^{[lower-alpha 2]} (kpc³) are selected in various directions. All the stars in these volumes are counted and the total number of stars statistically determined. The number of globular clusters, dust clouds, and interstellar gas is determined in a similar fashion. To determine the number of galaxies in superclusters, volumes in cubic megaparsecs^{[lower-alpha 2]} (Mpc³) are selected. All the galaxies in these volumes are classified and tallied. The total number of galaxies can then be determined statistically. The huge Boötes void is measured in cubic megaparsecs.^[18]

In cosmology, volumes of cubic gigaparsecs^{[lower-alpha 2]} (Gpc³) are selected to determine the distribution of matter in the visible universe and to determine the number of galaxies and quasars. The Sun is the only star in its cubic parsec,^{[lower-alpha 2]} (pc³) but in globular clusters the stellar density could be from 100 to 1000 per cubic parsec.

Notes

1. error of approximately one part per billion (1×10⁻⁹) for this calculation

2. 1 pc^3	≈ 2.938×10^49 m^3
   1 kpc^3	≈ 2.938×10^58 m^3
   1 Mpc^3	≈ 2.938×10^67 m^3
   1 Gpc^3	≈ 2.938×10^76 m^3
   1 Tpc³	≈ 2.938×10^85 m^3

References

1. "Cosmic Distance Scales - The Milky Way". Retrieved 24 September 2014.
2. Benedict, G. F.; et al. "Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri" (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
3. Dyson, F. W. (March 1913). "Stars, Distribution and drift of, The distribution in space of the stars in Carrington's Circumpolar Catalogue". Monthly Notices of the Royal Astronomical Society. 73: 334–342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334. There is a need for a name for this unit of distance. Mr. Charlier has suggested Siriometer ... Professor Turner suggests parsec, which may be taken as an abbreviated form of 'a distance corresponding to a parallax of one second'.
4. Cox, Arthur N., ed. (2000). Allen's Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book.....C. ISBN 0387987460.
5. Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2.
6. High Energy Astrophysics Science Archive Research Center (HEASARC). "Deriving the Parallax Formula". NASA's Imagine the Universe!. Astrophysics Science Division (ASD) at NASA's Goddard Space Flight Center. Retrieved 26 November 2011.
7. Bessel, F. W. (1838). "Bestimmung der Entfernung des 61sten Sterns des Schwans" [Determination of the distance of the 61st star of Cygnus]. Astronomische Nachrichten. 16: 65–96.
8. International Astronomical Union, ed. (31 August 2012), "RESOLUTION B2 on the re-definition of the astronomical unit of length" (PDF), RESOLUTION B2, Beijing: International Astronomical Union, The XXVIII General Assembly of International Astronomical Union recommends [adopted] that the astronomical unit be redefined to be a conventional unit of length equal to exactly 149597870700 m, in agreement with the value adopted in IAU 2009 Resolution B2
9. "Four Resolutions to be Presented for Voting at the IAU XXIX GA".
10. Pogge, Richard. "Astronomy 162". Ohio State University.
11. "Parallax Measurements". jrank.org.
12. "The Hipparcos Space Astrometry Mission". Retrieved 28 August 2007.
13. Turon, Catherine. "From Hipparchus to Hipparcos".
14. "GAIA". European Space Agency.
15. "Galaxy structures: the large scale structure of the nearby universe". Retrieved 22 May 2007.
16. Mei, S.; Blakeslee, J. P.; Côté, P.; et al. (2007). "The ACS Virgo Cluster Survey. XIII. SBF Distance Catalog and the Three-dimensional Structure of the Virgo Cluster". The Astrophysical Journal. 655: 144. Bibcode:2007ApJ...655..144M. doi:10.1086/509598.
17. Lineweaver, Charles H.; Davis, Tamara M. (2005-03-01). "Misconceptions about the Big Bang". Archived from the original on 2011-08-10. Retrieved 2016-02-04.
18. Kirshner, R. P.; Oemler, A., Jr.; Schechter, P. L.; Shectman, S. A. (1981). "A million cubic megaparsec void in Bootes". The Astrophysical Journal. 248: L57. doi:10.1086/183623. ISSN 0004-637X.

External links

• Guidry, Michael. "Astronomical Distance Scales". Astronomy 162: Stars, Galaxies, and Cosmology. University of Tennessee, Knoxville. Retrieved 26 March 2010.
• Merrifield, Michael. "pc Parsec". Sixty Symbols. Brady Haran for the University of Nottingham.