Rank-dependent expected utility

The rank-dependent expected utility model (originally called anticipated utility) is a generalized expected utility model of choice under uncertainty, designed to explain the behaviour observed in the Allais paradox, as well as for the observation that many people both purchase lottery tickets (implying risk-loving preferences) and insure against losses (implying risk aversion).

A natural explanation of these observations is that individuals overweight low-probability events such as winning the lottery, or suffering a disastrous insurable loss. In the Allais paradox, individuals appear to forgo the chance of a very large gain to avoid a one per cent chance of missing out on an otherwise certain large gain, but are less risk averse when offered the chance of reducing an 11 per cent chance of loss to 10 per cent.

A number of attempts were made to model preferences incorporating probability theory, most notably the original version of prospect theory, presented by Daniel Kahneman and Amos Tversky (1979). However, all such models involved violations of first-order stochastic dominance. In prospect theory, violations of dominance were avoided by the introduction of an 'editing' operation, but this gave rise to violations of transitivity.

The crucial idea of rank-dependent expected utility was to overweight only unlikely extreme outcomes, rather than all unlikely events. Formalising this insight required transformations to be applied to the cumulative probability distribution function, rather than to individual probabilities (Quiggin, 1982, 1993).

The central idea of rank-dependent weightings was then incorporated by Daniel Kahneman and Amos Tversky into prospect theory, and the resulting model was referred to as cumulative prospect theory (Tversky & Kahneman, 1992).

Formal representation

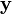As the name implies, the rank-dependent model is applied to the increasing rearrangement \mathbf{y}_{[ \; ]} of \mathbf{y} which satisfies y_{[1]}\leq y_{[2]}\leq ...\leq y_{[S]}.

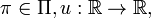W(\mathbf{y})=\sum_{s\in \Omega }h_{[s]}(\mathbf{\pi })u(y_{[s]}) where \mathbf{\pi }\in \Pi ,u:\mathbb{R} \rightarrow \mathbb{R} , and h_{[s]}( \mathbf{\pi }) is a probability weight such that h_{[s]}(\mathbf{\pi })=q\left( \sum\limits_{t=1}^{s}\pi _{[t]}\right) -q\left( \sum\limits_{t=1}^{s-1}\pi _{[t]}\right)

for a transformation function q:[0,1]\rightarrow [0,1] with q(0)=0, q(1)=1 .

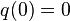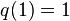Note that \sum_{s\in \Omega }h_{[s]}(\mathbf{\pi })=q\left( \sum\limits_{t=1}^{S}\pi _{[t]}\right) =q(1)=1 so that the decision weights sum to 1.

References

See also

This article is issued from Wikipedia - version of the 3/8/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.