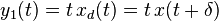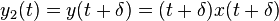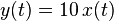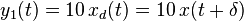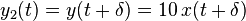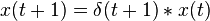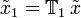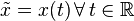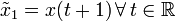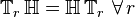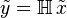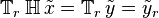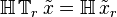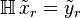Time-invariant system
A time-invariant (TIV) system is a system whose output does not depend explicitly on time. Such systems are regarded as a class of systems in the field of system analysis. Lack of time dependence is captured in the following mathematical property of such a system:
- If the input signal
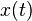 produces an output
produces an output 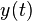 then any time shifted input,
then any time shifted input, 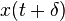 , results in a time-shifted output
, results in a time-shifted output 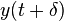
This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output.
In the context of a system schematic, this property can also be stated as follows:
- If a system is time-invariant then the system block commutes with an arbitrary delay.
If a time-invariant system is also linear, it is the subject of LTI system theory (linear time-invariant) with direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. Nonlinear time-invariant systems lack a comprehensive, governing theory. Discrete time-invariant systems are known as shift-invariant systems. Systems which lack the time-invariant property are studied as time-variant systems.
Simple example
To demonstrate how to determine if a system is time-invariant, consider the two systems:
- System A:
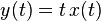
- System B:
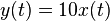
Since system A explicitly depends on t outside of 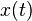 and
and 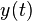 , it is not time-invariant. System B, however, does not depend explicitly on t so it is time-invariant.
, it is not time-invariant. System B, however, does not depend explicitly on t so it is time-invariant.
Formal example
A more formal proof of why systems A and B above differ is now presented. To perform this proof, the second definition will be used.
System A:
- Start with a delay of the input
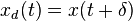
- Now delay the output by
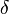
- Clearly
 , therefore the system is not time-invariant.
, therefore the system is not time-invariant.
System B:
- Start with a delay of the input
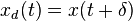
- Now delay the output by
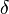
- Clearly
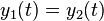 , therefore the system is time-invariant.
, therefore the system is time-invariant.
Abstract example
We can denote the shift operator by 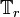 where
where  is the amount by which a vector's index set should be shifted. For example, the "advance-by-1" system
is the amount by which a vector's index set should be shifted. For example, the "advance-by-1" system
can be represented in this abstract notation by
where 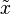 is a function given by
is a function given by
with the system yielding the shifted output
So 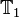 is an operator that advances the input vector by 1.
is an operator that advances the input vector by 1.
Suppose we represent a system by an operator 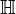 . This system is time-invariant if it commutes with the shift operator, i.e.,
. This system is time-invariant if it commutes with the shift operator, i.e.,
If our system equation is given by
then it is time-invariant if we can apply the system operator 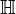 on
on 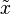 followed by the shift operator
followed by the shift operator 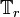 , or we can apply the shift operator
, or we can apply the shift operator 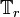 followed by the system operator
followed by the system operator 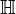 , with the two computations yielding equivalent results.
, with the two computations yielding equivalent results.
Applying the system operator first gives
Applying the shift operator first gives
If the system is time-invariant, then