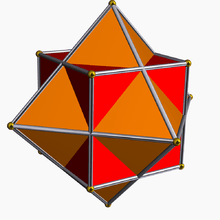
Compound of cube and octahedron
| Compound of cube and octahedron | |
|---|---|
 | |
| Type | Compound |
| Coxeter diagram | |
| Stellation core | cuboctahedron |
| Convex hull | Rhombic dodecahedron |
| Index | W43 |
| Polyhedra | 1 octahedron 1 cube |
| Faces | 8 triangles 6 squares |
| Edges | 24 |
| Vertices | 14 |
| Symmetry group | octahedral (Oh) |
This polyhedron can be seen as either a polyhedral stellation or a compound.
As a compound
It can be seen as the compound of an octahedron and a cube. It is one of four compounds constructed from a Platonic solid or Kepler-Poinsot polyhedron and its dual.
It has octahedral symmetry (Oh) and shares the same vertices as a rhombic dodecahedron.
As a stellation
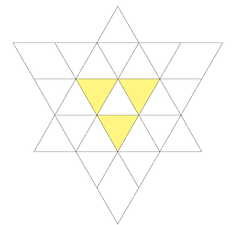
It is also the first stellation of the cuboctahedron and given as Wenninger model index 43.
It can be seen as a cuboctahedron with square and triangular pyramids added to each face.
The stellation facets for construction are:
References
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 978-0-521-09859-5.
This article is issued from Wikipedia - version of the 9/17/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.