Homothetic transformation

Two similar geometric figures related by a homothetic transformation with respect to a homothetic center S. The angles at corresponding points are the same and have the same sense; for example, the angles ABC and A'B'C' are both clockwise and equal in magnitude.

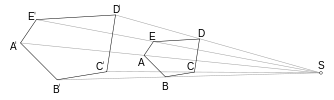
In mathematics, a homothety (or homothecy, or homogeneous dilation) is a transformation of an affine space determined by a point S called its center and a nonzero number λ called its ratio, which sends

$M\mapsto S+\lambda {\overrightarrow {SM}},$

in other words it fixes S, and sends any M to another point N such that the segment SN is on the same line as SM, but scaled by a factor λ.^[1] In Euclidean geometry homotheties are the similarities that fix a point and either preserve (if λ > 0) or reverse (if λ < 0) the direction of all vectors. Together with the translations, all homotheties of an affine (or Euclidean) space form a group, the group of dilations or homothety-translations. These are precisely the affine transformations with the property that the image of every line L is a line parallel to L.

In projective geometry, a homothetic transformation is a similarity transformation (i.e., fixes a given elliptic involution) that leaves the line at infinity pointwise invariant.^[2]

In Euclidean geometry, a homothety of ratio λ multiplies distances between points by |λ| and all areas by λ². The first number is called the ratio of magnification or dilation factor or scale factor or similitude ratio. Such a transformation can be called an enlargement if the scale factor exceeds 1. The above-mentioned fixed point S is called homothetic center or center of similarity or center of similitude

Homothety and uniform scaling

If the homothetic center S happens to coincide with the origin O of the vector space (S ≡ O), then every homothety with scale factor λ is equivalent to a uniform scaling by the same factor, which sends

${\overrightarrow {OM}}\mapsto \lambda {\overrightarrow {OM}}.$

As a consequence, in the specific case in which S ≡ O, the homothety becomes a linear transformation, which preserves not only the collinearity of points (straight lines are mapped to straight lines), but also vector addition and scalar multiplication.

The image of a point (x, y) after a homothety with center (a, b) and scale factor λ is given by (a + λ(x − a), b + λ(y − b)).

See also

• Scaling (geometry) a similar notion in vector spaces
• Homothetic center, the center of a homothetic transformation taking one of a pair of shapes into the other
• The Hadwiger conjecture on the number of strictly smaller homothetic copies of a convex body that may be needed to cover it
• Homothetic function (economics), a function of the form f(U(y)) in which U is a homogeneous function and f is a monotonically increasing function.

Notes

1. Hadamard (, p. 145)
2. Tuller (, p. 119)

References

• Hadamard, J., Lessons in Plane Geometry.
• Meserve, Bruce E. (1955), "Homothetic transformations", Fundamental Concepts of Geometry, Addison-Wesley, pp. 166–169.
• Tuller, Annita, A Modern Introduction to Geometries.

External links

• Homothety, interactive applet from Cut-the-Knot.