Orthoptic (geometry)
In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.
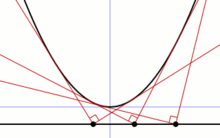
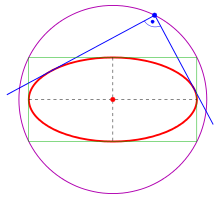

- Examples
The orthoptic of
- 1) a parabola is its directrix (proof: s. parabola),
- 2) an ellipse is the director circle (s. below),
- 3) a hyperbola is the circle (in case of there are no orthogonal tangents, s. below),
- 4) an astroid is a quadrifolium with the polar equation
- (s. below).
- Generalizations
- 1) An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (s. below).
- 2) An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.
- 3) Thales' theorem on a chord can be considered as the orthoptic of two circles which are degenerated to the two points .
Remark: In medicine there exists the term orthoptic, too.
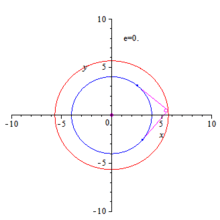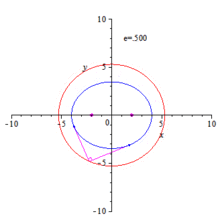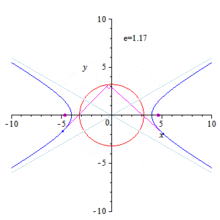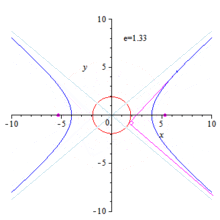
Orthoptic of an ellipse and hyperbola
Ellipse
The ellipse with equation can be represented by the unusual parametric representation[1]
where is the slope of the tangent at a point of the ellipse. describes the upper half and the lower half of the ellipse. The points ) with tangents parallel to the y-axis are excluded. But this is no problem, because these tangents meet orthogonal the tangents parallel to the x-axis in the ellipse points Hence the points are points of the desired orthoptic (circle ).
The tangent at point has the equation
If a tangent contains the point , off the ellipse, then the equation
holds. Eliminatig the square root leads to
which has two solutions corresponding to the two tangents passing point . The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at point orthogonal, the following equations hold:
The last equation is equivalent to
This means:
- The intersection points of orthogonal tangents are points of the circle .
Hyperbola
The ellipse case can be adopted nearly literally to the hyperbola case. The only changes to be made are: 1) replace by and 2) restrict by . One gets:
- The intersection points of orthogonal tangents are points of the circle .
Orthoptic of an astroid

An astroid can be described by the parametric representation
- .
From the condition one recognizes, at what distance in parameter space an orthogonal tangent to appears. It turns out, that the distance is independent of parameter , namely . The equations of the (orthogonal) tangents at the points and are:
- .
Their common point has coordinates:
- ,
- .
This is at the same time a parametric representation of the orthoptic.
Elimination of parameter yields the implicit representation
Introducing the new parameter one gets
- . (proof uses Angle sum and difference identities.)
Herefrom we get the polar representation
of the orthoptic. Hence
- The orthoptic of an astroid is a quadrifolium.
Isoptic of a parabola, an ellipse and a hyperbola
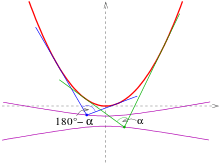
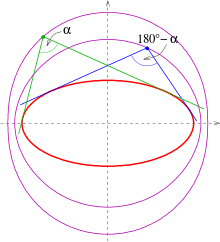

Below isotopics for an angle are listed. They are called -isoptics. For the proofs: s. below.
Equations of the isoptics
- parabola :
The -isoptics of the parabola with equation are the arms of the hyperbola
The arms of the hyperbola provide the isoptics for the two angles (s. picture).
- Ellipse:
The -isoptics of the ellipse with equation are the two parts of the curve of 4. degree
- (s. picture).
- Hyperbola:
The -isoptics of the hyperbola with the equation are the two parts of the curve of 4. degree
Proofs
- Parabola:
A parabola can be parametrized by the slope of its tangents :
The tangent with slope has the equation
Point is on the tangent, if
holds. That means, the slopes of the two tangents containing fulfill the quadratic equation
If the tangents meet with angle or , the equation
has to be fulfilled. Solving the quadratic equation for inserting into the last equation, one gets
This is the equation of the hyperbola above. Its arms bear the two isoptics of the parabola for the two angles and .
- Ellipse:
In case of an ellipse one can adopt the idea for the orthoptic until the quadratic equation
Now, as in case of a parabola, the quadratic equation has to be solved and the two solutions to be inserted into the equation . Rearranging shows that the isoptics are parts of the curve of 4. degree:
- Hyperbola:
The solution for the case of a hyperbola can be adopted from the ellipse case by replacing by (as in the case of the orthoptics, s. above).
Remark: For visualizing the isoptics see implicit curve.
External links
| Wikimedia Commons has media related to Isoptics. |
- Special Plane Curves.
- Mathworld
- Jan Wassenaar's Curves
- "Courbe Isoptique" at Encyclopédie des Formes Mathématiques Remarquables (in French)
- "Courbe Orthoptique" at Encyclopédie des Formes Mathématiques Remarquables (in French)
Notes
- ↑ P. K. Jain: Textbook of Analytical Geometry of two Dimensions. p. 214.
References
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5.
- Boris Odehnal: Equioptic Curves of Conic Sections. Journal for Geometry and Graphics, Volume 14 (2010), No. 1, p. 29–43.
- Hermann Schaal: Lineare Algebra und Analytische Geometrie. Band III, Vieweg, 1977, ISBN 3 528 03058 5, p. 220.
- Jacob Steiner’s Vorlesungen über synthetische Geometrie. B. G. Teubner, Leipzig 1867 (bei Google Books), 2. Teil, p. 186.
- Maurizio Ternullo: Two new sets of ellipse related concyclic points. Journal of Geometry 2009, 94, p. 159–173.