Pursuit curve
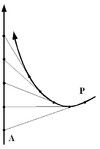
A curve of pursuit is a curve constructed by analogy to having a point or points representing pursuers and pursuees; the curve of pursuit is the curve traced by the pursuers.
With the paths of the pursuer and pursuee parameterized in time, the pursuee is always on the pursuer's tangent. That is, given F(t) the pursuer (follower) and L(t) the pursued (leader), for every t with F′(t) ≠ 0 there is an x such that
Single pursuer
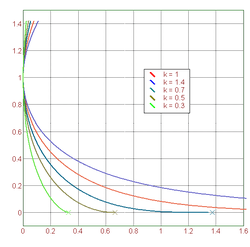
The path followed by a single pursuer, following a pursuee that moves at constant speed on a line, is a radiodrome. It is a solution of the differential equation 1+y' ² = k² (a−x²) y" ².
Multiple pursuers

Typical drawings of curves of pursuit have each point acting as both pursuer and pursuee, inside a polygon, and having each pursuer pursue the adjacent point on the polygon. An example of this is the mice problem.
See also
External links
| Wikimedia Commons has media related to Curve of pursuit. |
- Mathworld, with a slightly narrower definition that |L′(t)| and |F′(t)| are constant
- MacTutor Pursuit curve