Squircle
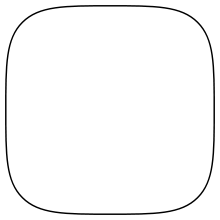
A squircle is a mathematical shape intermediate between a square and a circle. It is a special case of a superellipse. The word "squircle" is a portmanteau of the words "square" and "circle".
Equation
In a Cartesian coordinate system, the squircle centred on the point (a, b) with axes parallel to the coordinate axes is described by the equation:[1]
where r is the minor radius of the squircle (cf. equation of a circle).
The case that is centred on the origin (that is, with a = b = 0) is called Lamé's special quartic.
The same equation expressed in polar coordinates, using the sign function , is:
Generalisation
The squircle is a specific case (found by setting n = 4) of the class of shapes known as "supercircles", which have the equation
Unfortunately, the taxonomy is not consistent - some authors refer to the class as "supercircles" and the specific case as a squircle, while others adopt the opposite naming convention. Supercircles in turn are a subset of the even more general "superellipses", which have the equation
where ra and rb are the semi-major and semi-minor axes. Superellipses were extensively studied and popularized by the Danish mathematician Piet Hein.
Area
The area inside the squircle can be expressed as the area of a superellipse with n = 4 in terms of the gamma function, Γ(x), as
where r is the minor radius of the squircle.
By replacing 1/4! and 1/2! with their respective values it is found that
where S is the lemniscate constant.
Similar shapes

A shape similar to a squircle, called a rounded square, may be generated by separating four quarters of a circle and connecting their loose ends with straight lines. Such a shape is very similar but not identical to the squircle. Although constructing a rounded square may be conceptually and physically simpler, the squircle has the simpler equation and can be generalised much more easily. One consequence of this is that the squircle and other superellipses can be scaled up or down quite easily. This is useful where, for example, one wishes to create nested squircles.

Another similar shape is a truncated circle, the boundary of the intersection of the regions enclosed by a square and by a concentric circle whose diameter is both greater than the length of the side of the square and less than the length of the diagonal of the square (so that each figure has interior points that are not in the interior of the other). Such shapes lack the tangent continuity possessed by both superellipses and rounded squares.
Uses
Squircles are useful in optics. If light is passed through a two-dimensional square aperture, the central spot in the diffraction pattern can be closely modelled by a squircle or supercircle. If a rectangular aperture is used, the spot can be approximated by a superellipse.[2]
Squircles have also been used to construct dinner plates. A squircular plate has a larger area (and can thus hold more food) than a circular one with the same radius, but still occupies the same amount of space in a rectangular or square cupboard. This is even more true of a square plate, but there are various problems (such as fragility, and difficulty of wiping up sauce[3]) associated with the corners of square plates.[4]
Sumvision manufactures an SD card-based MP3 player named Squircle for the budget market. It is not, however, a genuine squircle, although vaguely similar in shape.[5]
Nokia is closely associated with the squircle, having used it as a touchpad button in many phones.[6][7]
See also
References
- ↑ Weisstein, Eric W. "Squircle". MathWorld.
- ↑ M. Fernández Guasti; A. Meléndez Cobarrubias; F.J. Renero Carrillo; A. Cornejo Rodríguez (2005). "LCD pixel shape and far-field diffraction patterns" (PDF). Optik. 116 (6): 265–269. doi:10.1016/j.ijleo.2005.01.018. Retrieved 20 November 2006.
- ↑ Goss, Mr. (1989-08-14). Missing or empty
|title=(help) - ↑ "Squircle Plate". Kitchen Contraptions. Retrieved 20 November 2006.
- ↑ "Squircle SD Card MP3 Player". Advanced MP3 Players. Retrieved 20 November 2006.
- ↑ Nokia Designer Mark Delaney mentions the squircle in a video regarding classic Nokia phone designs:
Nokia 6700 – The little black dress of phones. Retrieved 9 December 2009.See 3:13 in video
- ↑ "Clayton Miller evaluates shapes on mobile phone platforms". Retrieved 2 July 2011.
External links
| Wikimedia Commons has media related to Squircle. |