Stabilizing selection

These charts depict the different types of genetic selection. On each graph, the x-axis variable is the type of phenotypic trait and the y-axis variable is the amount of organisms. Group A is the original population and Group B is the population after selection. Graph 1 shows directional selection, in which a single extreme phenotype is favored. Graph 2 depicts stabilizing selection, where the intermediate phenotype is favored over the extreme traits. Graph 3 shows disruptive selection, in which the extreme phenotypes are favored over the intermediate.

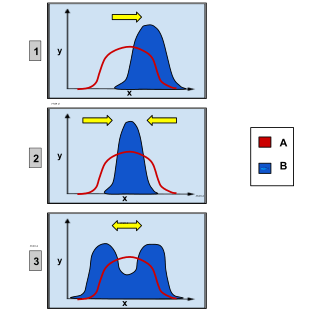
Stabilizing selection (not the same thing as negative selection^[1][2]) is a type of natural selection in which genetic diversity decreases and the population mean stabilizes on a particular trait value. This is thought to be the most common mechanism of action for natural selection because most traits do not appear to change drastically over time.^[3] Stabilizing selection commonly uses negative selection (a.k.a. purifying selection) to select against extreme values of the character. Stabilizing selection is the opposite of disruptive selection. Instead of favoring individuals with extreme phenotypes, it favors the intermediate variants. It reduces phenotypic variation and maintains the status quo. Natural selection tends to remove the more severe phenotypes, resulting in the reproductive success of the norm or average phenotypes.^[4] Because most traits change little over time, stabilizing selection is thought to be the most common type of selection in most populations. ^[5] However, a meta-analysis of studies that measured selection in the wild failed to find an overall trend for stabilizing selection. ^[6] The reason can be that methods for detecting stabilizing selection are complex. They can involve studying the changes that causes natural selection in the mean and variance of the trait, or measuring fitness for a range of different phenotypes under natural conditions and examining the relationship between these fitness measurements and the trait value, but analysis and interpretation of the results is not straightforward. ^[7]

Examples

Human birth weight

A classic example of this is human birth weight. Babies of low weight lose heat more quickly and get ill from infectious diseases more easily, whereas babies of large body weight are more difficult to deliver through the pelvis. Infants of a more medium weight survive much more often. For the larger or smaller babies, the baby mortality rate is much higher.^[8] The bell curve of the human population peaks at a birth weight that the newly born babies exhibit the minimum death rate.

Plant height

Another example of a trait, that might be acted on by stabilizing selection, is plant height. A plant that is too short may not be able to compete with other plants for sunlight. However, extremely tall plants may be more susceptible to wind damage. Combined, these two selection pressures select to maintain plants of medium height. The number of plants of medium height will increase while the numbers of short and tall plants will decrease.^[9]

Butterfly's wing eyespots

The African butterfly Bicyclus anynana exhibits stabilizing selection with its wing eyespots.^[10] It has been suggested that the circular eyespots positioned on the wings are favoured functionally compared to other shapes and sizes.^[11]

A chart showing three models for selection

See also

• Balancing selection
• Koinophilia
• Directional selection
• Frequency-dependent foraging by pollinators
• Assortative mating
• Hypergamy
• Fluctuating selection

Citations

1. Lemey, Philippe; Marco Salemi; Anne-Mieke Vandamme (2009). The Phylogenetic Handbook. Cambridge University Press. ISBN 978-0-521-73071-6.
2. http://www.nature.com/scitable/topicpage/Negative-Selection-1136
3. Charlesworth B, Lande R, Slatkin M (1982) "A neo-Darwinian commentary on macroevolution." Evolution 36-3 http://www.jstor.org/discover/10.2307/2408095
4. Campbell, Neil A.; Reece, Jane B. (2002). "Biology". Benjamin Cummings: 450–451
5. Charlesworth B, Lande R, Slatkin M (1982) "A neo-Darwinian commentary on macro-evolution." Evolution 36-3 http://www.jstor.org/discover/10.2307/2408095
6. Kingsolver JG, Hoekstra HE, Hoekstra J, Berrigan D, Vignieri SN, Hill CE, Hoang A, Gilbert P, Beerli P. (2001) "The Strength of Super Genetic Selection in Natural Populations." The American Naturalist 157-3 http://www.oeb.harvard.edu/faculty/hoekstra/pdfs/kingsolver2001amnat.pdf
7. Lande R and Arnold SJ. (1983) "The Measurement of Selection on Correlated Characters." Evolution 37-6
8. https://www.mun.ca/biology/scarr/Stabilizing_Selection_in_Humans.html
9. http://www.sparknotes.com/biology/evolution/naturalselection/section1.rhtml
10. Brakefield, Paul M., Patrícia Beldade, and Bas J. Zwaan. "The African butterfly Bicyclus anynana: a model for evolutionary genetics and evolutionary developmental biology." Cold Spring Harbor Protocols 2009.5 (2009): pdb-emo122.
11. http://www.nature.com/hdy/journal/v80/n3/full/6883660a.html

References

• Campbell, Neil A.; Reece, Jane B. (2002). "Biology". Benjamin Cummings: 450–451
• Lemey, Philippe; Marco Salemi; Anne-Mieke Vandamme (2009). The Phylogenetic Handbook. Cambridge University Press. ISBN 978-0-521-73071-6.
• http://www.nature.com/scitable/topicpage/Negative-Selection-1136
• Sheets HD, Mitchell CE (2001). "Why the null matters: statistical tests, random walks and evolution". Genetica. 112-113: 105–25. doi:10.1023/A:1013308409951. PMID 11838761.
• McDonald JH, Kreitman M (1991). "Adaptive protein evolution at the Adh locus in Drosophila". Nature. 351 (6328): 652–4. doi:10.1038/351652a0. PMID 1904993.
• Pheasant, M.; Mattick, S. (Sep 2007). "Raising the estimate of functional human sequences" (Free full text). Genome Research. 17 (9): 1245–1253. doi:10.1101/gr.6406307. ISSN 1088-9051. PMID 17690206.
• Zhang, R.; Peng, Y.; Wang, W.; Su, B. (May 2007). "Rapid evolution of an X-linked microRNA cluster in primates" (Free full text). Genome Research. 17 (5): 612–617. doi:10.1101/gr.6146507. ISSN 1088-9051. PMC 1855169. PMID 17416744.