Well-known text

Well-known text (WKT) is a text markup language for representing vector geometry objects on a map, spatial reference systems of spatial objects and transformations between spatial reference systems. A binary equivalent, known as well-known binary (WKB), is used to transfer and store the same information on databases. The formats were originally defined by the Open Geospatial Consortium (OGC) and described in their Simple Feature Access and Coordinate Transformation Service specifications. The current standard definition is in the ISO/IEC 13249-3:2016 standard, "Information technology – Database languages – SQL multimedia and application packages – Part 3: Spatial" (SQL/MM) and ISO 19162:2015, "Geographic information – Well-known text representation of coordinate reference systems".

Geometric objects

WKT can represent 18 distinct geometric objects:

Coordinates for geometries may be 2D (x, y), 3D (x, y, z), 4D (x, y, z, m) with an m value that is part of a linear referencing system or 2D with an m value (x, y, m). Three-dimensional geometries are designated by a "Z" after the geometry type and geometries with a linear referencing system have an "M" after the geometry type. Empty geometries that contain no coordinates can be specified by using the symbol EMPTY after the type name.

WKT geometries are used throughout OGC specifications and are present in applications that implement these specifications. For example, PostGIS contains functions that can convert geometries to and from a WKT representation, making them human readable.

It's useful to note that the OGC standard definition requires a polygon to be topologically closed. It also states that if the exterior linear ring of a polygon is defined in a counter clockwise direction it will be seen from the "top". Any interior linear rings should be defined in opposite fashion compared to the exterior ring, in this case, clockwise.[1]

Geometry primitives (2D)
Type Examples
Point POINT (30 10)
LineString 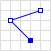LINESTRING (30 10, 10 30, 40 40)
Polygon 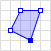POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10))
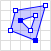POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10),
(20 30, 35 35, 30 20, 20 30))
Multipart geometries (2D)
Type Examples
MultiPoint 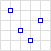MULTIPOINT ((10 40), (40 30), (20 20), (30 10))
MULTIPOINT (10 40, 40 30, 20 20, 30 10)
MultiLineString 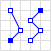MULTILINESTRING ((10 10, 20 20, 10 40),
(40 40, 30 30, 40 20, 30 10))
MultiPolygon 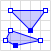MULTIPOLYGON (((30 20, 45 40, 10 40, 30 20)),
((15 5, 40 10, 10 20, 5 10, 15 5)))
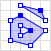MULTIPOLYGON (((40 40, 20 45, 45 30, 40 40)),
((20 35, 10 30, 10 10, 30 5, 45 20, 20 35),
(30 20, 20 15, 20 25, 30 20)))

The following are some other examples of geometric WKT strings: (Note: Each item below is an individual geometry.)

GEOMETRYCOLLECTION(POINT(4 6),LINESTRING(4 6,7 10))
POINT ZM (1 1 5 60)
POINT M (1 1 80)
POINT EMPTY
MULTIPOLYGON EMPTY
CIRCULARSTRING(1 5, 6 2, 7 3)
COMPOUNDCURVE(CIRCULARSTRING(0 0,1 1,1 0),(1 0,0 1))
CURVEPOLYGON(CIRCULARSTRING(-2 0,-1 -1,0 0,1 -1,2 0,0 2,-2 0),(-1 0,0 0.5,1 0,0 1,-1 0))
MULTICURVE((5 5,3 5,3 3,0 3),CIRCULARSTRING(0 0,2 1,2 2))
TRIANGLE((0 0 0,0 1 0,1 1 0,0 0 0))
TIN (((0 0 0, 0 0 1, 0 1 0, 0 0 0)), ((0 0 0, 0 1 0, 1 1 0, 0 0 0)))
POLYHEDRALSURFACE Z (
    ((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)),
    ((0 0 0, 0 1 0, 0 1 1, 0 0 1, 0 0 0)),
    ((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),
    ((1 1 1, 1 0 1, 0 0 1, 0 1 1, 1 1 1)),
    ((1 1 1, 1 0 1, 1 0 0, 1 1 0, 1 1 1)),
    ((1 1 1, 1 1 0, 0 1 0, 0 1 1, 1 1 1))
  )

Well-known binary

Well-known binary (WKB) representations are typically shown in hexadecimal strings.

The first byte indicates the byte order for the data:

The second part is an integer for the geometry type, as described below:

Geometry types, and WKB integer codes
Type 2D Z M ZM
Geometry 0000 1000 2000 3000
Point 0001 1001 2001 3001
LineString 0002 1002 2002 3002
Polygon 0003 1003 2003 3003
MultiPoint 0004 1004 2004 3004
MultiLineString 0005 1005 2005 3005
MultiPolygon 0006 1006 2006 3006
GeometryCollection 0007 1007 2007 3007
CircularString 0008 1008 2008 3008
CompoundCurve 0009 1009 2009 3009
CurvePolygon 0010 1010 2010 3010
MultiCurve 0011 1011 2011 3011
MultiSurface 0012 1012 2012 3012
Curve 0013 1013 2013 3013
Surface 0014 1014 2014 3014
PolyhedralSurface 0015 1015 2015 3015
TIN 0016 1016 2016 3016
Triangle 0017 1017 2017 3017

Each data type has a unique data structure, such as the number of points or linear rings, followed by coordinates in double-precision floating-point format (double).

For example, the geometry POINT(2.0 4.0) is represented as: 000000000140000000000000004010000000000000, where:

Coordinate reference systems

WKT can describe coordinate reference systems. This WKT format was initially defined by the Open Geospatial Consortium in 1999, then extended in 2001. This format is sometime known as "WKT 1".[2] Later, evolution of the Coordinate Reference System conceptual model, new requirements and inconsistencies in implementation of WKT 1 format between different software[3] have encouraged the revision of that format. The updated "Well-known text representation of coordinate reference systems" standard, sometime known as "WKT 2", was adopted by the Open Geospatial Consortium in 2015.[4] This standard is published conjointly by the International Organization for Standardization as ISO 19162:2015.[5]

For example the WKT below describes a two-dimensional geographic coordinate reference system with a latitude axis first, then a longitude axis. The coordinate system is related to Earth by the WGS84 geodetic datum:

GEODCRS["WGS 84",
  DATUM["World Geodetic System 1984",
    ELLIPSOID["WGS 84", 6378137, 298.257223563, LENGTHUNIT["metre", 1]]],
  CS[ellipsoidal, 2],
    AXIS["Latitude (lat)“, north, ORDER[1]],
    AXIS["Longitude (lon)“, east, ORDER[2]],
    ANGLEUNIT[”degree", 0.0174532925199433]]

The WKT format can describe not only geographic coordinate reference systems, but also geocentric, projected, vertical, temporal and engineering ones (for example a coordinate reference system attached to a boat). The standard describes how to combine those coordinate reference systems together.

Backward compatibility

A software capable to read coordinate reference systems in WKT 2 format can also read many (but not all) equivalent systems in WKT 1 format.[6] Some caveats exist, notably the removal of the TOWGS84 element [7] which is replaced by the BOUNDCRS element. Another caveat is about the units of measurement. Some of them were unspecified in oldest WKT 1 specifications (for example the PRIMEM unit), which has led to different interpretations by different software. Those units of measurement have been clarified in the 2001 update and the WKT 2 specification is consistent with that clarification. But not all software have followed the 2001 clarification.

Coordinate operations

A WKT format is defined to describe the operation methods and parameters used to convert or transform coordinates between two different coordinate reference systems. The WKT 1 and WKT 2 formats are incompatible regarding coordinate operations, because of differences in the modelling.[8] Below is an example of a concatenation of two WKT 1 transformation descriptions, where the Mercator projection is applied first and then an affine transform is applied on the result:

CONCAT_MT[
  PARAM_MT["Mercator_2SP",
    PARAMETER["semi_major",6370997.0],
    PARAMETER["semi_minor",6370997.0],
    PARAMETER["central_meridian",180.0],
    PARAMETER["false_easting",-500000.0],
    PARAMETER["false_northing",-1000000.0],
    PARAMETER["standard parallel 1",60.0]],
  PARAM_MT["Affine",
    PARAMETER["num_row",3],
    PARAMETER["num_col",3],
    PARAMETER["elt_0_1",1],
    PARAMETER["elt_0_2",2],
    PARAMETER["elt 1 2",3]]]

Below is an example of a datum shift operation in WKT 2 format. Contrarily to an equivalent description in WKT 1 format, the WKT 2 description specifies the source and target coordinate reference systems, together with the domain of validity and the accuracy (in metres) that we can expect from this operation:

COORDINATEOPERATION["AGD84 to GDA94 Auslig 5m",
  SOURCECRS[…full CRS definition required here but omitted for brevity…],
  TARGETCRS[…full CRS definition required here but omitted for brevity…],
  METHOD["Geocentric translations", ID["EPSG", 1031]],
  PARAMETER["X-axis translation", -128.5, LENGTHUNIT["metre", 1]],
  PARAMETER["Y-axis translation",  -53.0, LENGTHUNIT["metre", 1]],
  PARAMETER["Z-axis translation",  153.4, LENGTHUNIT["metre", 1]]
  OPERATIONACCURACY[5],
  AREA["Australia onshore"],
  BBOX[-43.7, 112.85, -9.87, 153.68]]

RDBMS Engines that provide support

APIs that provide support

Protocols that provide support

Variations

See also

References

  1. ↑ See the OGC Implementation Specification for geographic information – Simple Feature Access, section 6.1.11.1. http://www.opengeospatial.org/standards/sfa
  2. ↑ "Well-Known Text format (WKT) version 1". www.geoapi.org. Retrieved 2016-11-01.
  3. ↑ "OGC 12-063r5 Annex E". docs.opengeospatial.org. Retrieved 2016-10-01.
  4. ↑ "OGC 12-063r5". docs.opengeospatial.org. Retrieved 2015-05-06.
  5. ↑ "ISO 19162:2015". www.iso.org. Retrieved 2016-11-01.
  6. ↑ "OGC 12-063r5 Backward compatibility". docs.opengeospatial.org. Retrieved 2016-10-01.
  7. ↑ "OGC 12-063r5 Annex C.3.3". docs.opengeospatial.org. Retrieved 2016-10-01.
  8. ↑ "OGC 12-063r5 Annex C.4.5". docs.opengeospatial.org. Retrieved 2016-10-01.
  9. ↑ Solr GEO support
  10. ↑ https://docs.marklogic.com/guide/search-dev/geospatial
  11. ↑ http://docs.memsql.com/docs/geospatial-guide
  12. ↑ Well-Known Text (WKT) Format, MySQL documentation
  13. ↑ H2 create spatial index documentation
  14. ↑ https://github.com/postgis/postgis/blob/2.1.0/doc/ZMSgeoms.txt
  15. ↑ http://postgis.org/docs/ST_GeomFromEWKT.html
  16. ↑ http://www.osgeo.org/files/mapguide/docs/2.0/da/dc0/group___agf_text.htm

External links

This article is issued from Wikipedia - version of the 11/7/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.