Vertex arrangement

For the local description of faces around a vertex of a polyhedron or tiling, see vertex figure.

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.

For example, a square vertex arrangement is understood to mean four points in a plane, equal distance and angles from a center point.

Two polytopes share the same vertex arrangement if they share the same 0-skeleton.

Vertex arrangement

The same set of vertices can be connected by edges in different ways. For example, the pentagon and pentagram have the same vertex arrangement, while the second connects alternate vertices.

Two polygons with same vertex arrangement.

pentagon
pentagram

A vertex arrangement is often described by the convex hull polytope which contains it. For example, the regular pentagram can be said to have a (regular) pentagonal vertex arrangement.

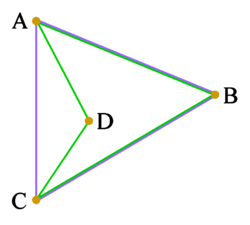ABCD is a concave quadrilateral (green). Its vertex arrangement is the set {A, B, C, D}. Its convex hull is the triangle ABC (blue). The vertex arrangement of the convex hull is the set {A, B, C}, which is not the same as that of the quadrilateral; so here, the convex hull is not a way to describe the vertex arrangement.

Infinite tilings can also share common vertex arrangements.

For example, this triangular lattice of points can be connected to form either isosceles triangles or rhombic faces.

Four tilings with same vertex arrangement.

Lattice points
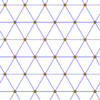Triangular tiling
rhombic tiling
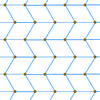Zig-zag rhombic tiling
Rhombille tiling

Edge arrangement

Polyhedra can also share an edge arrangement while differing in their faces.

For example, the self-intersecting great dodecahedron shares its edge arrangement with the convex icosahedron:

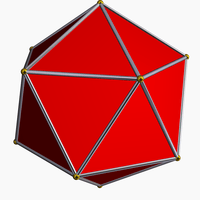Two polyhedra with same edge arrangement.

icosahedron
(20 triangles)
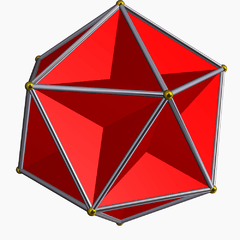great dodecahedron
(12 intersecting pentagons)

Face arrangement

4-polytopes can also have the same face arrangement which means they have similar vertex, edge, and face arrangements, but may differ in their cells.

For example, of the ten nonconvex regular Schläfli-Hess polychora, there are only 7 unique face arrangements.

For example, the grand stellated 120-cell and great stellated 120-cell, both with pentagrammic faces, appear visually indistinguishable without a representation of their cells:

Two (projected) polychora with same face arrangement

Grand stellated 120-cell
(120 small stellated dodecahedra)
Great stellated 120-cell
(120 great stellated dodecahedra)

Classes of similar polytopes

George Olshevsky advocates the term regiment for a set of polytopes that share an edge arrangement, and more generally n-regiment for a set of polytopes that share elements up to dimension n. Synonyms for special cases include company for a 2-regiment (sharing faces) and army for a 0-regiment (sharing vertices).

See also

External links

This article is issued from Wikipedia - version of the 9/10/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.