Small stellated dodecahedron

Small stellated dodecahedron
Type	Kepler–Poinsot polyhedron
Stellation core	regular dodecahedron
Elements	F = 12, E = 30 V = 12 (χ = -6)
Faces by sides	125
Schläfli symbol	{5/2,5}
Wythoff symbol	5 | 25/2
Coxeter diagram
Symmetry group	Ih, H3, [5,3], (*532)
References	U34, C43, W20
Properties	Regular nonconvex
(5/2)^5 (Vertex figure)	Great dodecahedron (dual polyhedron)

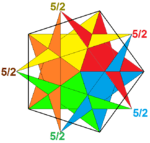
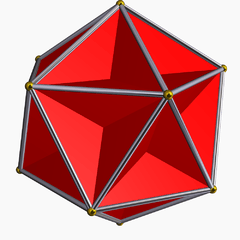
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5/2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

It shares the same vertex arrangement as the convex regular icosahedron. It also shares the same edge arrangement with the great icosahedron.

It is the second of four stellations of the dodecahedron.

If the pentagrammic faces are considered as 5 triangular faces, it shares the same surface topology as the pentakis dodecahedron, but with much taller isosceles triangle faces, with the height of the pentagonal pyramids adjusted so that the five triangles in the pentagram become coplanar.

If we regard it as having 12 pentagrams as faces, with these pentagrams meeting at 30 edges and 12 vertices, we can compute its genus using Euler's formula

${\displaystyle V-E+F=2-2g}$

and conclude that the small stellated dodecahedron has genus 4. This observation, made by Louis Poinsot, was initially confusing, but Felix Klein showed in 1877 that the small stellated dodecahedron could be seen as a branched covering of the Riemann sphere by a Riemann surface of genus 4, with branch points at the center of each pentagram. In fact this Riemann surface, called Bring's curve, has the greatest number of symmetries of any Riemann surface of genus 4: the symmetric group $S_{5}$ acts as automorphisms^[1]

Images

Transparent model	Handmade models
(See also: animated)
Spherical tiling	Stellation	Net
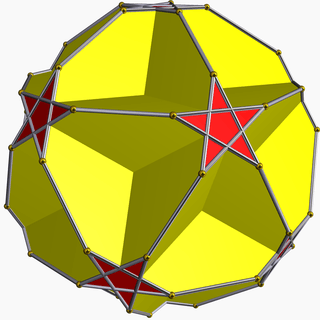
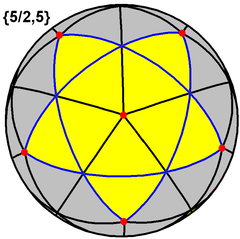This polyhedron also represents a spherical tiling with a density of 3. (One spherical pentagram face, outlined in blue, filled in yellow)	It can also be constructed as the first of three stellations of the dodecahedron, and referenced as Wenninger model [W20].	× 12 Small stellated dodecahedra can be constructed out of paper or cardstock by connecting together 12 five-sided isosceles pyramids in the same manner as the pentagons in a regular dodecahedron. With an opaque material, this visually represents the exterior portion of each pentagrammic face.

In art

Floor mosaic by Paolo Uccello, 1430

• It can also be seen in a floor mosaic in St Mark's Basilica, Venice by Paolo Uccello circa 1430.
• It is central to two lithographs by M. C. Escher: Contrast (Order and Chaos) (1950) and Gravitation (1952).

Related polyhedra

Its convex hull is the regular convex icosahedron. It also shares its edges with the great icosahedron.

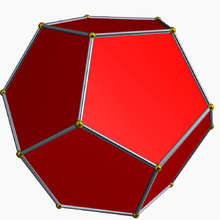
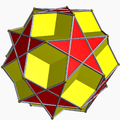
This polyhedron is the truncation of the great dodecahedron:

The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping (as truncated pentagrams).

Name	Small stellated dodecahedron	Truncated small stellated dodecahedron	Dodecadodecahedron	Truncated great dodecahedron	Great dodecahedron
Coxeter-Dynkin diagram
Picture

See also

• Compound of small stellated dodecahedron and great dodecahedron

References

1. Weber, Matthias (2005). "Kepler's small stellated dodecahedron as a Riemann surface". Pacific J. Math. 220. pp. 167–182. pdf

• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
• Weber, Matthias (2005), "Kepler's small stellated dodecahedron as a Riemann surface", Pacific J. Math., 220: 167–182

External links

• Eric W. Weisstein, Small stellated dodecahedron (Uniform polyhedron) at MathWorld.
  • Weisstein, Eric W. "DodecahedronStellations". MathWorld.

• Uniform polyhedra and duals

Stellations of the dodecahedron
Platonic solid	Kepler–Poinsot solids
Dodecahedron	Small stellated dodecahedron	Great dodecahedron	Great stellated dodecahedron