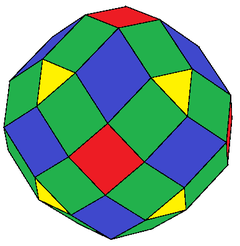
Expanded cuboctahedron

Expanded cuboctahedron
Schläfli symbolrr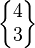\begin{Bmatrix} 4 \\ 3 \end{Bmatrix} = rrr{4,3}
Conway notationedaC = aaaC
Faces50:
8 {3}
6+24 {4}
12 rhombs
Edges96
Vertices48
Symmetry groupOh, [4,3], (*432) order 48
Rotation groupO, [4,3]+, (432), order 24
Dual polyhedronDeltoidal tetracontaoctahedron
Propertiesconvex

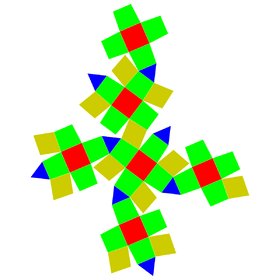Net

The expanded cuboctahedron is a polyhedron, constructed as a expanded cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.

It can also be constructed as a rectified rhombicuboctahedron.

Other names

Expansion

The expansion operation from the rhombic dodecahedron can be seen in this animation:

Dissection

Excavated expanded cuboctahedron
Faces86:
8 {3}
6+24+48 {4}
Edges168
Vertices62
Euler characteristic-20
genus11
Symmetry groupOh, [4,3], (*432) order 48

This polyhedron can be dissected into a central rhombic dodecahedron surrounded by: 12 rhombic prisms, 8 tetrahedra, 6 square pyramids, and 24 triangular prisms.

If the central rhombic dodecahedron and the 12 rhombic prisms are removed, you can create a toroidal polyhedron with all regular polygon faces.[1] This toroid has 86 faces (8 triangles and 78 squares), 168 edges, and 62 vertices. 14 of the 62 vertices are on the interior, defining the removed central rhombic dodecahedron. With Euler characteristic χ = f + v - e = -20, its genus, g = (2-χ)/2 is 11.

Related polyhedra

Name Cube Cubocta-
hedron		 Rhombi-
cuboctahedron		 Expanded
cuboctahedron
Coxeter[2] C CO = rC rCO = rrC rrCO = rrrC
Conway aC = aO eC eaC
Image
Conway O = dC jC oC oaC
Dual

See also

References

  1. ↑ A Dissection of the Expanded Rhombic Dodecahedron
  2. ↑ http://mathworld.wolfram.com/UniformPolyhedron.html

External links

This article is issued from Wikipedia - version of the 3/3/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.