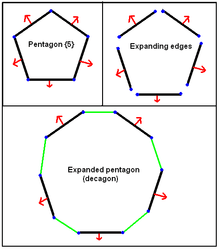
Expansion (geometry)

In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements (vertices, edges, etc.). Equivalently this operation can be imagined by keeping facets in the same position but reducing their size.
The expansion of a regular polytope creates a uniform polytope, but the operation can be applied to any convex polytope, as demonstrated for polyhedra in Conway polyhedron notation. For polyhedra, an expanded polyhedron has all the faces of the original polyhedron, all the faces of the dual polyhedron, and new square faces in place of the original edges.
Expansion of regular polytopes
According to Coxeter, this multidimensional term was defined by Alicia Boole Stott[1] for creating new polytopes, specifically starting from regular polytopes to construct new uniform polytopes.
The expansion operation is symmetric with respect to a regular polytope and its dual. The resulting figure contains the facets of both the regular and its dual, along with various prismatic facets filling the gaps created between intermediate dimensional elements.
It has somewhat different meanings by dimension. In a Wythoff construction, an expansion is generated by reflections from the first and last mirrors. In higher dimensions, lower dimensional expansions can be written with a subscript, so e2 is the same as t0,2 in any dimension.
By dimension:
- A regular {p} polygon expands into a regular 2n-gon.
- The operation is identical to truncation for polygons, e{p} = e1{p} = t0,1{p} = t{p} and has Coxeter-Dynkin diagram

 .
.
- The operation is identical to truncation for polygons, e{p} = e1{p} = t0,1{p} = t{p} and has Coxeter-Dynkin diagram
- A regular {p,q} polyhedron (3-polytope) expands into a polyhedron with vertex figure p.4.q.4.
- This operation for polyhedra is also called cantellation, e{p,q} = e2{p,q} = t0,2{p,q} = rr{p,q}, and has Coxeter diagram



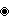 .
.
-
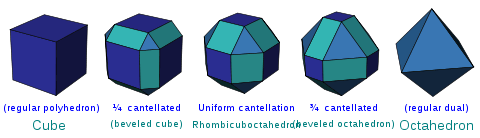
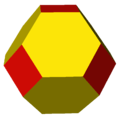
- For example, a rhombicuboctahedron can be called an expanded cube, expanded octahedron, as well as a cantellated cube or cantellated octahedron.
-
- This operation for polyhedra is also called cantellation, e{p,q} = e2{p,q} = t0,2{p,q} = rr{p,q}, and has Coxeter diagram
- A regular {p,q,r} 4-polytope (4-polytope) expands into a new 4-polytope with the original {p,q} cells, new cells {r,q} in place of the old vertices, p-gonal prisms in place of the old faces, and r-gonal prisms in place of the old edges.
- This operation for 4-polytopes is also called runcination, e{p,q,r} = e3{p,q,r} = t0,3{p,q,r}, and has Coxeter diagram
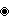





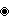 .
.
- This operation for 4-polytopes is also called runcination, e{p,q,r} = e3{p,q,r} = t0,3{p,q,r}, and has Coxeter diagram
- Similarly a regular {p,q,r,s} 5-polytope expands into a new 5-polytope with facets {p,q,r}, {s,r,q}, {p,q}×{ } prisms, {s,r}×{ } prisms, and {p}×{s} duoprisms.
- This operation is called sterication, e{p,q,r,s} = e4{p,q,r,s} = t0,4{p,q,r,s} = 2r2r{p,q,r,s} and has Coxeter diagram







 .
.
- This operation is called sterication, e{p,q,r,s} = e4{p,q,r,s} = t0,4{p,q,r,s} = 2r2r{p,q,r,s} and has Coxeter diagram
The general operator for expansion of a regular n-polytope is t0,n-1{p,q,r,...}. New regular facets are added at each vertex, and new prismatic polytopes are added at each divided edge, face, ... ridge, etc.
See also
Notes
- ↑ Coxeter, Regular Polytopes (1973), p. 123. p.210
References
- Coxeter, H. S. M., Regular Polytopes. 3rd edition, Dover, (1973) ISBN 0-486-61480-8.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
| Seed | Truncation | Rectification | Bitruncation | Dual | Expansion | Omnitruncation | Alternations | ||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |