Mean longitude

Mean longitude is the ecliptic longitude at which an orbiting body could be found if its orbit were circular and free of perturbations. While nominally a simple longitude, in practice the mean longitude is a hybrid angle.^[1]

Definition

An orbiting body's mean longitude is calculated l = Ω + ω + M, where Ω is the longitude of the ascending node, ω is the argument of the pericenter and M is the mean anomaly, the body's angular distance from the pericenter as if it moved with constant speed rather than with the variable speed of an elliptical orbit. Its true longitude is calculated similarly, L = Ω + ω + ν, where ν is the true anomaly.

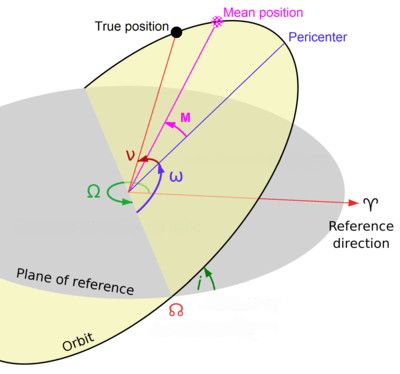
• Define a reference direction, ♈, along the ecliptic. Typically, this is the direction of the vernal equinox. At this point, ecliptic longitude is 0°.
• The body's orbit is generally inclined to the ecliptic, therefore define the angular distance from ♈ to the place where the orbit crosses the ecliptic from south to north as the longitude of the ascending node, Ω.
• Define the angular distance along the plane of the orbit from the ascending node to the pericenter as the argument of the pericenter, ω.
• Define the mean anomaly, M, as the angular distance from the pericenter which the body would have if it moved in a circular orbit, in the same orbital period as the actual body in its elliptical orbit.

From these definitions, the mean longitude, l, is the angular distance the body would have from the reference direction if it moved with uniform speed,

l = Ω + ω + M,

measured along the ecliptic from ♈ to the ascending node, then up along the plane of the body's orbit to its mean position.^[2]

Discussion

Mean longitude, like mean anomaly, does not measure an angle between any physical objects. It is simply a convenient uniform measure of how far around its orbit a body has progressed since passing the reference direction. While mean longitude measures a mean position and assumes constant speed, true longitude meausures the actual longitude and assumes the body has moved with its actual speed, which varies around its elliptical orbit. The difference between the two is known as the equation of the center.^[3]

Formulae

From the above definitions, define the longitude of the pericenter

ϖ = Ω + ω.

Then mean longitude is also^[1]

l = ϖ + M.

Another form often seen is the mean longitude at epoch, ε. This is simply the mean longitude at a reference time t₀, known as the epoch. Mean longitude can then be expressed,^[2]

l = ε + n(t − t₀), or

l = ε + nt, since t = 0 at the epoch t₀.

where n is the mean angular motion and t is any arbitrary time. In some sets of orbital elements, ε is one of the six elements.^[2]

See also

• Mean motion
• Orbital elements
• True longitude

References

1. Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. pp. 197–198. ISBN 0-943396-35-2.
2. Smart, W. M. (1977). Textbook on Spherical Astronomy (sixth ed.). Cambridge University Press, Cambridge. p. 122. ISBN 0-521-29180-1.
3. Meeus, Jean (1991). p. 222