Pentagrammic crossed-antiprism
| Uniform Pentagrammic crossed-antiprism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 12, E = 20 V = 10 (χ = 2) |
| Faces by sides | 10{3}+2{5/2} |
| Schläfli symbol | s{2,10/3} sr{2,5/3} |
| Wythoff symbol | | 2 2 5/3 |
| Coxeter diagram | = |
| Symmetry | D5h, [5,2], (*522), order 20 |
| Rotation group | D5, [5,2]+, (552), order 10 D5d |
| Index references | U80(a) |
| Dual | Pentagrammic concave trapezohedron |
| Properties | nonconvex |
 Vertex figure 3.3.3.5/3 or 3.3.3.-5/2 | |
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams.
This polyhedron is identified with the indexed name U80 as a uniform polyhedron.
 An alternative representation with hollow pentagrams. |
The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron.
 Pentagrammic crossed-antiprism |
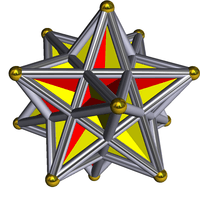 Great icosahedron coloured with D5d symmetry |
See also
External links
- http://www.mathconsult.ch/showroom/unipoly/80.html
- http://bulatov.org/polyhedra/uniform/u05.html
- http://www.math.technion.ac.il/~rl/kaleido/data/05.html
This article is issued from Wikipedia - version of the 12/10/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.