Great icosahedron
| Great icosahedron | |
|---|---|
 | |
| Type | Kepler–Poinsot polyhedron |
| Stellation core | icosahedron |
| Elements | F = 20, E = 30 V = 12 (χ = 2) |
| Faces by sides | 20{3} |
| Schläfli symbol | {3,5/2} |
| Wythoff symbol | 5/2 | 2 3 |
| Coxeter diagram | |
| Symmetry group | Ih, H3, [5,3], (*532) |
| References | U53, C69, W41 |
| Properties | Regular nonconvex deltahedron |
 (35)/2 (Vertex figure) |
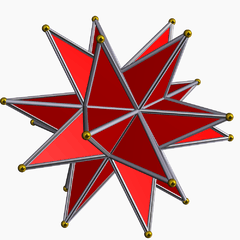 Great stellated dodecahedron (dual polyhedron) |
In geometry, the great icosahedron is one of four Kepler-Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol {3,5/2} and Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
. It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
Images
| Transparent model | Density | Stellation diagram | Net |
|---|---|---|---|
 A transparent model of the great icosahedron (See also Animation) |
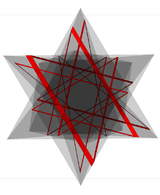 It has a density of 7, as shown in this cross-section. |
 It is a stellation of the icosahedron, counted by Wenninger as model [W41] and the 16th of 17 stellations of the icosahedron and 7th of 59 stellations by Coxeter. |
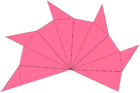 × 12 × 12Net (surface geometry); twelve isosceles pentagrammic pyramids, arranged like the faces of a dodecahedron. Each pyramid folds up like a fan: the dotted lines fold the opposite direction from the solid lines. |
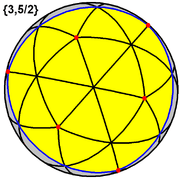 This polyhedron represents a spherical tiling with a density of 7. (One spherical triangle face is shown above, outlined in blue, filled in yellow) |
As a snub
The great icosahedron can be constructed a uniform snub, with different colored faces and only tetrahedral symmetry: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . This construction can be called a retrosnub tetrahedron or retrosnub tetratetrahedron,[1] similar to the snub tetrahedron symmetry of the icosahedron, as a partial faceting of the truncated octahedron (or omnitruncated tetrahedron):
. This construction can be called a retrosnub tetrahedron or retrosnub tetratetrahedron,[1] similar to the snub tetrahedron symmetry of the icosahedron, as a partial faceting of the truncated octahedron (or omnitruncated tetrahedron): ![]()
![]()
![]()
![]()
![]() . It can also be constructed with 2 colors of triangles and pyritohedral symmetry as,
. It can also be constructed with 2 colors of triangles and pyritohedral symmetry as, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and is called a retrosnub octahedron.
, and is called a retrosnub octahedron.
| Tetrahedral | Pyritohedral |
|---|---|
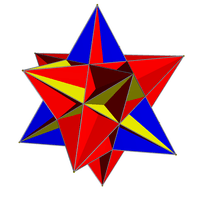 |
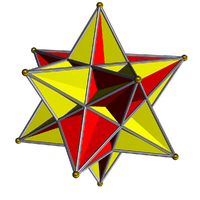 |
Related polyhedra
It shares the same vertex arrangement as the regular convex icosahedron. It also shares the same edge arrangement as the small stellated dodecahedron.
A truncation operation, repeatedly applied to the great icosahedron, produces a sequence of uniform polyhedra. Truncating edges down to points produces the great icosidodecahedron as a rectified great icosahedron. The process completes as a birectification, reducing the original faces down to points, and producing the great stellated dodecahedron.
The truncated great stellated dodecahedron is a degenerate polyhedron, with 20 triangular faces from the truncated vertices, and 12 (hidden) doubled up pentagonal faces ({10/2}) as truncations of the original pentagram faces, the latter forming two great dodecahedra inscribed within and sharing the edges of the icosahedron.
| Name | Great stellated dodecahedron |
Truncated great stellated dodecahedron | Great icosidodecahedron |
Truncated great icosahedron |
Great icosahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
|||||
| Picture |  |
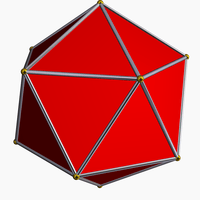 |
 |
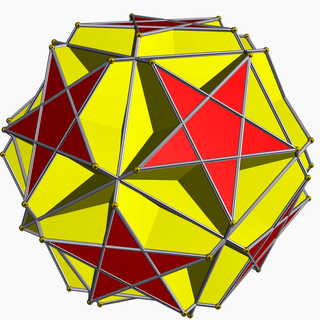 |
 |
References
- ↑ Klitzing, Richard. "uniform polyhedra Great icosahedron".
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3. MR 676126. (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104
External links
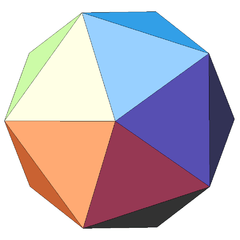
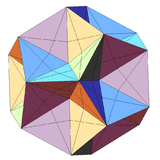
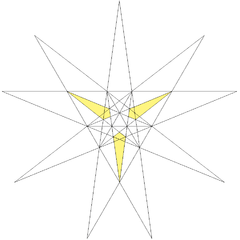
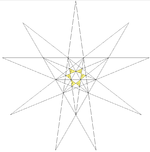
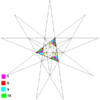
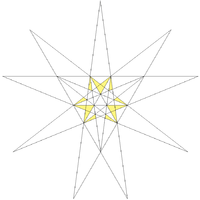
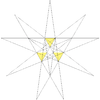
| Notable stellations of the icosahedron | |||||||||
| Regular | Uniform duals | Regular compounds | Regular star | Others | |||||
| (Convex) icosahedron | Small triambic icosahedron | Medial triambic icosahedron | Great triambic icosahedron | Compound of five octahedra | Compound of five tetrahedra | Compound of ten tetrahedra | Great icosahedron | Excavated dodecahedron | Final stellation |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. | |||||||||