Spatial analysis
Spatial analysis or spatial statistics includes any of the formal techniques which study entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques, many still in their early development, using different analytic approaches and applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is the technique applied to structures at the human scale, most notably in the analysis of geographic data.
Complex issues arise in spatial analysis, many of which are neither clearly defined nor completely resolved, but form the basis for current research. The most fundamental of these is the problem of defining the spatial location of the entities being studied.
Classification of the techniques of spatial analysis is difficult because of the large number of different fields of research involved, the different fundamental approaches which can be chosen, and the many forms the data can take.
History of spatial analysis
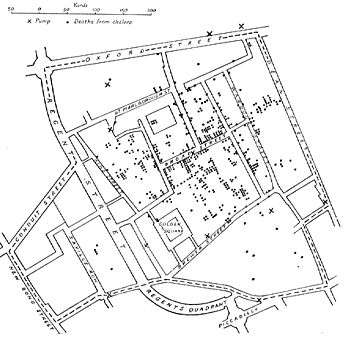
Spatial analysis can perhaps be considered to have arisen with early attempts at cartography and surveying but many fields have contributed to its rise in modern form. Biology contributed through botanical studies of global plant distributions and local plant locations, ethological studies of animal movement, landscape ecological studies of vegetation blocks, ecological studies of spatial population dynamics, and the study of biogeography. Epidemiology contributed with early work on disease mapping, notably John Snow's work of mapping an outbreak of cholera, with research on mapping the spread of disease and with location studies for health care delivery. Statistics has contributed greatly through work in spatial statistics. Economics has contributed notably through spatial econometrics. Geographic information system is currently a major contributor due to the importance of geographic software in the modern analytic toolbox. Remote sensing has contributed extensively in morphometric and clustering analysis. Computer science has contributed extensively through the study of algorithms, notably in computational geometry. Mathematics continues to provide the fundamental tools for analysis and to reveal the complexity of the spatial realm, for example, with recent work on fractals and scale invariance. Scientific modelling provides a useful framework for new approaches.
Fundamental issues in spatial analysis
Spatial analysis confronts many fundamental issues in the definition of its objects of study, in the construction of the analytic operations to be used, in the use of computers for analysis, in the limitations and particularities of the analyses which are known, and in the presentation of analytic results. Many of these issues are active subjects of modern research.
Common errors often arise in spatial analysis, some due to the mathematics of space, some due to the particular ways data are presented spatially, some due to the tools which are available. Census data, because it protects individual privacy by aggregating data into local units, raises a number of statistical issues. The fractal nature of coastline makes precise measurements of its length difficult if not impossible. A computer software fitting straight lines to the curve of a coastline, can easily calculate the lengths of the lines which it defines. However these straight lines may have no inherent meaning in the real world, as was shown for the coastline of Britain.
These problems represent a challenge in spatial analysis because of the power of maps as media of presentation. When results are presented as maps, the presentation combines spatial data which are generally accurate with analytic results which may be inaccurate, leading to an impression that analytic results are more accurate than the data would indicate.[1]
Spatial characterization

The definition of the spatial presence of an entity constrains the possible analysis which can be applied to that entity and influences the final conclusions that can be reached. While this property is fundamentally true of all analysis, it is particularly important in spatial analysis because the tools to define and study entities favor specific characterizations of the entities being studied. Statistical techniques favor the spatial definition of objects as points because there are very few statistical techniques which operate directly on line, area, or volume elements. Computer tools favor the spatial definition of objects as homogeneous and separate elements because of the limited number of database elements and computational structures available, and the ease with which these primitive structures can be created.
Spatial dependency or auto-correlation
Spatial dependency is the co-variation of properties within geographic space: characteristics at proximal locations appear to be correlated, either positively or negatively. Spatial dependency leads to the spatial autocorrelation problem in statistics since, like temporal autocorrelation, this violates standard statistical techniques that assume independence among observations. For example, regression analyses that do not compensate for spatial dependency can have unstable parameter estimates and yield unreliable significance tests. Spatial regression models (see below) capture these relationships and do not suffer from these weaknesses. It is also appropriate to view spatial dependency as a source of information rather than something to be corrected.[2]
Locational effects also manifest as spatial heterogeneity, or the apparent variation in a process with respect to location in geographic space. Unless a space is uniform and boundless, every location will have some degree of uniqueness relative to the other locations. This affects the spatial dependency relations and therefore the spatial process. Spatial heterogeneity means that overall parameters estimated for the entire system may not adequately describe the process at any given location.
Scaling
Spatial measurement scale is a persistent issue in spatial analysis; more detail is available at the modifiable areal unit problem (MAUP) topic entry. Landscape ecologists developed a series of scale invariant metrics for aspects of ecology that are fractal in nature. In more general terms, no scale independent method of analysis is widely agreed upon for spatial statistics.
Sampling
Spatial sampling involves determining a limited number of locations in geographic space for faithfully measuring phenomena that are subject to dependency and heterogeneity. Dependency suggests that since one location can predict the value of another location, we do not need observations in both places. But heterogeneity suggests that this relation can change across space, and therefore we cannot trust an observed degree of dependency beyond a region that may be small. Basic spatial sampling schemes include random, clustered and systematic. These basic schemes can be applied at multiple levels in a designated spatial hierarchy (e.g., urban area, city, neighborhood). It is also possible to exploit ancillary data, for example, using property values as a guide in a spatial sampling scheme to measure educational attainment and income. Spatial models such as autocorrelation statistics, regression and interpolation (see below) can also dictate sample design.
Common errors in spatial analysis
The fundamental issues in spatial analysis lead to numerous problems in analysis including bias, distortion and outright errors in the conclusions reached. These issues are often interlinked but various attempts have been made to separate out particular issues from each other.[3]
Length
In a paper by Benoit Mandelbrot on the coastline of Britain it was shown that it is inherently nonsensical to discuss certain spatial concepts despite an inherent presumption of the validity of the concept. Lengths in ecology depend directly on the scale at which they are measured and experienced. So while surveyors commonly measure the length of a river, this length only has meaning in the context of the relevance of the measuring technique to the question under study.
-
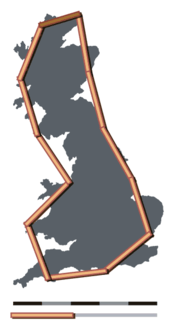
Britain measured using a long yardstick
-
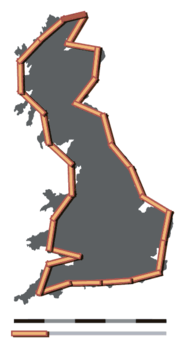
Britain measured using a medium yardstick
-
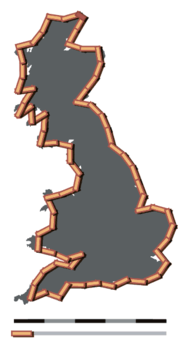
Britain measured using a short yardstick
Locational fallacy
The locational fallacy refers to error due to the particular spatial characterization chosen for the elements of study, in particular choice of placement for the spatial presence of the element.
Spatial characterizations may be simplistic or even wrong. Studies of humans often reduce the spatial existence of humans to a single point, for instance their home address. This can easily lead to poor analysis, for example, when considering disease transmission which can happen at work or at school and therefore far from the home.
The spatial characterization may implicitly limit the subject of study. For example, the spatial analysis of crime data has recently become popular but these studies can only describe the particular kinds of crime which can be described spatially. This leads to many maps of assault but not to any maps of embezzlement with political consequences in the conceptualization of crime and the design of policies to address the issue.
Atomic fallacy
This describes errors due to treating elements as separate 'atoms' outside of their spatial context. The fallacy is about transferring individual conclusions to spatial units.
Ecological fallacy
The ecological fallacy describes errors due to performing analyses on aggregate data when trying to reach conclusions on the individual units. Errors occur in part from spatial aggregation. For example, a pixel represents the average surface temperatures within an area. Ecological fallacy would be to assume that all points within the area have the same temperature. This topic is closely related to the modifiable areal unit problem.
Solutions to the fundamental issues
Geographic space

A mathematical space exists whenever we have a set of observations and quantitative measures of their attributes. For example, we can represent individuals' incomes or years of education within a coordinate system where the location of each individual can be specified with respect to both dimensions. The distances between individuals within this space is a quantitative measure of their differences with respect to income and education. However, in spatial analysis we are concerned with specific types of mathematical spaces, namely, geographic space. In geographic space, the observations correspond to locations in a spatial measurement framework that captures their proximity in the real world. The locations in a spatial measurement framework often represent locations on the surface of the Earth, but this is not strictly necessary. A spatial measurement framework can also capture proximity with respect to, say, interstellar space or within a biological entity such as a liver. The fundamental tenet is Tobler's First Law of Geography: if the interrelation between entities increases with proximity in the real world, then representation in geographic space and assessment using spatial analysis techniques are appropriate.
The Euclidean distance between locations often represents their proximity, although this is only one possibility. There are an infinite number of distances in addition to Euclidean that can support quantitative analysis. For example, "Manhattan" (or "Taxicab") distances where movement is restricted to paths parallel to the axes can be more meaningful than Euclidean distances in urban settings. In addition to distances, other geographic relationships such as connectivity (e.g., the existence or degree of shared borders) and direction can also influence the relationships among entities. It is also possible to compute minimal cost paths across a cost surface; for example, this can represent proximity among locations when travel must occur across rugged terrain.
Types of spatial analysis
Spatial data comes in many varieties and it is not easy to arrive at a system of classification that is simultaneously exclusive, exhaustive, imaginative, and satisfying. -- G. Upton & B. Fingelton[4]
Spatial data analysis
Urban and Regional Studies deal with large tables of spatial data obtained from censuses and surveys. It is necessary to simplify the huge amount of detailed information in order to extract the main trends. Multivariable analysis (or Factor analysis, FA) allows a change of variables, transforming the many variables of the census, usually correlated between themselves, into fewer independent "Factors" or "Principal Components" which are, actually, the eigenvectors of the data correlation matrix weighted by the inverse of their eigenvalues. This change of variables has two main advantages:
- Since information is concentrated on the first new factors, it is possible to keep only a few of them while losing only a small amount of information; mapping them produces fewer and more significant maps
- The factors, actually the eigenvectors, are orthogonal by construction, i.e. not correlated. In most cases, the dominant factor (with the largest eigenvalue) is the Social Component, separating rich and poor in the city. Since factors are not-correlated, other smaller processes than social status, which would have remained hidden otherwise, appear on the second, third, … factors.
Factor analysis depends on measuring distances between observations : the choice of a significant metric is crucial. The Euclidean metric (Principal Component Analysis), the Chi-Square distance (Correspondence Analysis) or the Generalized Mahalanobis distance (Discriminant Analysis ) are among the more widely used.[5] More complicated models, using communalities or rotations have been proposed.[6]
Using multivariate methods in spatial analysis began really in the 1950s (although some examples go back to the beginning of the century) and culminated in the 1970s, with the increasing power and accessibility of computers. Already in 1948, in a seminal publication, two sociologists, Bell and Shevky,[7] had shown that most city populations in the USA and in the world could be represented with three independent factors : 1- the « socio-economic status » opposing rich and poor districts and distributed in sectors running along highways from the city center, 2- the « life cycle », i.e. the age structure of households, distributed in concentric circles, and 3- « race and ethnicity », identifying patches of migrants located within the city. In 1961, in a groundbreaking study, British geographers used FA to classify British towns.[8] Brian J Berry, at the University of Chicago, and his students made a wide use of the method,[9] applying it to most important cities in the world and exhibiting common social structures.[10] The use of Factor Analysis in Geography, made so easy by modern computers, has been very wide but not always very wise.[11]
Since the vectors extracted are determined by the data matrix, it is not possible to compare factors obtained from different censuses. A solution consists in fusing together several census matrices in a unique table which, then, may be analyzed. This, however, assumes that the definition of the variables has not changed over time and produces very large tables, difficult to manage. A better solution, proposed by psychometricians,[12] groups the data in a « cubic matrix », with three entries (for instance, locations, variables, time periods). A Three-Way Factor Analysis produces then three groups of factors related by a small cubic « core matrix ».[13] This method, which exhibits data evolution over time, has not been widely used in geography.[14] In Los Angeles,[15] however, it has exhibited the role, traditionally ignored, of Downtown as an organizing center for the whole city during several decades.
Spatial autocorrelation
Spatial autocorrelation statistics measure and analyze the degree of dependency among observations in a geographic space. Classic spatial autocorrelation statistics include Moran's , Geary's , Getis's and the standard deviational ellipse. These statistics require measuring a spatial weights matrix that reflects the intensity of the geographic relationship between observations in a neighborhood, e.g., the distances between neighbors, the lengths of shared border, or whether they fall into a specified directional class such as "west". Classic spatial autocorrelation statistics compare the spatial weights to the covariance relationship at pairs of locations. Spatial autocorrelation that is more positive than expected from random indicate the clustering of similar values across geographic space, while significant negative spatial autocorrelation indicates that neighboring values are more dissimilar than expected by chance, suggesting a spatial pattern similar to a chess board.
Spatial autocorrelation statistics such as Moran's and Geary's are global in the sense that they estimate the overall degree of spatial autocorrelation for a dataset. The possibility of spatial heterogeneity suggests that the estimated degree of autocorrelation may vary significantly across geographic space. Local spatial autocorrelation statistics provide estimates disaggregated to the level of the spatial analysis units, allowing assessment of the dependency relationships across space. statistics compare neighborhoods to a global average and identify local regions of strong autocorrelation. Local versions of the and statistics are also available.
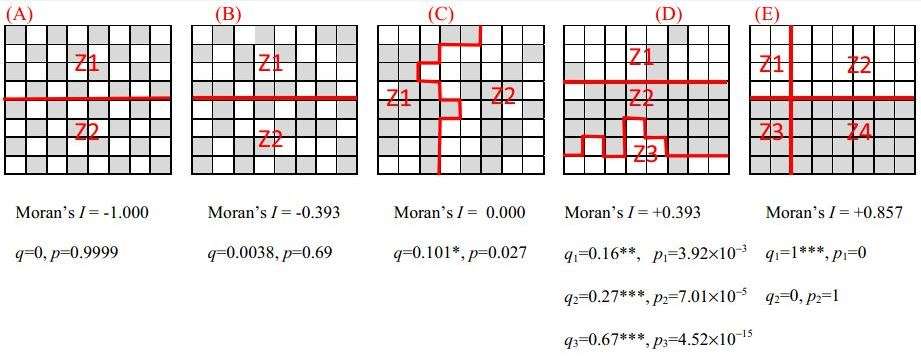
Spatial stratified heterogeneity
Spatial stratified heterogeneity, referring to the within-strata variance less than the between strata-variance, is ubiquitous in ecological phenomena, such as ecological zones and many ecological variables. Spatial stratified heterogeneity reflects the essence of nature, implies potential distinct mechanisms by strata, suggests possible determinants of the observed process, allows the representativeness of observations of the earth, and enforces the applicability of statistical inferences. Spatial stratified heterogeneity of an attribute can be measured by geographical detector q-statistic:[16]
where a population is partitioned into h = 1, ..., L strata; N stands for the size of the population, σ2 stands for variance of the attribute. The value of q is within [0, 1], 0 indicates no spatial stratified heterogeneity, 1 indicates perfect spatial stratified heterogeneity.The value of q indicates the percent of the variance of an attribute explained by the stratification.The q follows a noncentral F probability density function.
Spatial interpolation
Spatial interpolation methods estimate the variables at unobserved locations in geographic space based on the values at observed locations. Basic methods include inverse distance weighting: this attenuates the variable with decreasing proximity from the observed location. Kriging is a more sophisticated method that interpolates across space according to a spatial lag relationship that has both systematic and random components. This can accommodate a wide range of spatial relationships for the hidden values between observed locations. Kriging provides optimal estimates given the hypothesized lag relationship, and error estimates can be mapped to determine if spatial patterns exist.
Spatial regression
Spatial regression methods capture spatial dependency in regression analysis, avoiding statistical problems such as unstable parameters and unreliable significance tests, as well as providing information on spatial relationships among the variables involved. Depending on the specific technique, spatial dependency can enter the regression model as relationships between the independent variables and the dependent, between the dependent variables and a spatial lag of itself, or in the error terms. Geographically weighted regression (GWR) is a local version of spatial regression that generates parameters disaggregated by the spatial units of analysis.[17] This allows assessment of the spatial heterogeneity in the estimated relationships between the independent and dependent variables. The use of Bayesian hierarchical modeling[18] in conjunction with Markov Chain Monte Carlo (MCMC) methods have recently shown to be effective in modeling complex relationships using Poisson-Gamma-CAR, Poisson-lognormal-SAR, or Overdispersed logit models. Spatial stochastic processes, such as Gaussian processes are also increasingly being deployed in spatial regression analysis. Model-based versions of GWR, known as spatially varying coefficient models have been applied to conduct Bayesian inference.[18] Spatial stochastic process can become computationally effective and scalable Gaussian process models, such as Gaussian Predictive Processes[19] and Nearest Neighbor Gaussian Processes (NNGP).[20]
Spatial interaction
Spatial interaction or "gravity models" estimate the flow of people, material or information between locations in geographic space. Factors can include origin propulsive variables such as the number of commuters in residential areas, destination attractiveness variables such as the amount of office space in employment areas, and proximity relationships between the locations measured in terms such as driving distance or travel time. In addition, the topological, or connective, relationships between areas must be identified, particularly considering the often conflicting relationship between distance and topology; for example, two spatially close neighborhoods may not display any significant interaction if they are separated by a highway. After specifying the functional forms of these relationships, the analyst can estimate model parameters using observed flow data and standard estimation techniques such as ordinary least squares or maximum likelihood. Competing destinations versions of spatial interaction models include the proximity among the destinations (or origins) in addition to the origin-destination proximity; this captures the effects of destination (origin) clustering on flows. Computational methods such as artificial neural networks can also estimate spatial interaction relationships among locations and can handle noisy and qualitative data.
Simulation and modeling
Spatial interaction models are aggregate and top-down: they specify an overall governing relationship for flow between locations. This characteristic is also shared by urban models such as those based on mathematical programming, flows among economic sectors, or bid-rent theory. An alternative modeling perspective is to represent the system at the highest possible level of disaggregation and study the bottom-up emergence of complex patterns and relationships from behavior and interactions at the individual level.
Complex adaptive systems theory as applied to spatial analysis suggests that simple interactions among proximal entities can lead to intricate, persistent and functional spatial entities at aggregate levels. Two fundamentally spatial simulation methods are cellular automata and agent-based modeling. Cellular automata modeling imposes a fixed spatial framework such as grid cells and specifies rules that dictate the state of a cell based on the states of its neighboring cells. As time progresses, spatial patterns emerge as cells change states based on their neighbors; this alters the conditions for future time periods. For example, cells can represent locations in an urban area and their states can be different types of land use. Patterns that can emerge from the simple interactions of local land uses include office districts and urban sprawl. Agent-based modeling uses software entities (agents) that have purposeful behavior (goals) and can react, interact and modify their environment while seeking their objectives. Unlike the cells in cellular automata, simulysts can allow agents to be mobile with respect to space. For example, one could model traffic flow and dynamics using agents representing individual vehicles that try to minimize travel time between specified origins and destinations. While pursuing minimal travel times, the agents must avoid collisions with other vehicles also seeking to minimize their travel times. Cellular automata and agent-based modeling are complementary modeling strategies. They can be integrated into a common geographic automata system where some agents are fixed while others are mobile.
Multiple-point geostatistics (MPS)
Spatial analysis of a conceptual geological model is the main purpose of any MPS algorithm. The method analyzes the spatial statistics of the geological model, called the training image, and generates realizations of the phenomena that honor those input multiple-point statistics.
A recent MPS algorithm used to accomplish this task is the pattern-based method by Honarkhah.[21] In this method, a distance-based approach is employed to analyze the patterns in the training image. This allows the reproduction of the multiple-point statistics, and the complex geometrical features of the training image. Each output of the MPS algorithm is a realization that represents a random field. Together, several realizations may be used to quantify spatial uncertainty.
One of the recent methods is presented by Tahmasebi et al.[22] uses a cross-correlation function to improve the spatial pattern reproduction. They call their MPS simulation method as the CCSIM algorithm. This method is able to quantify the spatial connectivity, variability and uncertainty. Furthermore, the method is not sensitive to any type of data and is able to simulate both categorical and continuous scenarios. CCSIM algorithm is able to be used for any stationary, non-stationary and multivariate systems and it can provide high quality visual appeal model.,[23][24]
Geographic information science and spatial analysis
Geographic information systems (GIS) and the underlying geographic information science that advances these technologies have a strong influence on spatial analysis. The increasing ability to capture and handle geographic data means that spatial analysis is occurring within increasingly data-rich environments. Geographic data capture systems include remotely sensed imagery, environmental monitoring systems such as intelligent transportation systems, and location-aware technologies such as mobile devices that can report location in near-real time. GIS provide platforms for managing these data, computing spatial relationships such as distance, connectivity and directional relationships between spatial units, and visualizing both the raw data and spatial analytic results within a cartographic context.

Content
- Spatial location: Transfer positioning information of space objects with the help of space coordinate system. Projection transformation theory is the foundation of spatial object representation.
- Spatial distribution: the similar spatial object groups positioning information, including distribution, trends, contrast etc..
- Spatial form: the geometric shape of the spatial objects
- Spatial space: the space objects' approaching degree
- Spatial relationship: relationship between spatial objects, including topological, orientation, similarity, etc..
Geovisualization (GVis) combines scientific visualization with digital cartography to support the exploration and analysis of geographic data and information, including the results of spatial analysis or simulation. GVis leverages the human orientation towards visual information processing in the exploration, analysis and communication of geographic data and information. In contrast with traditional cartography, GVis is typically three- or four-dimensional (the latter including time) and user-interactive.
Geographic knowledge discovery (GKD) is the human-centered process of applying efficient computational tools for exploring massive spatial databases. GKD includes geographic data mining, but also encompasses related activities such as data selection, data cleaning and pre-processing, and interpretation of results. GVis can also serve a central role in the GKD process. GKD is based on the premise that massive databases contain interesting (valid, novel, useful and understandable) patterns that standard analytical techniques cannot find. GKD can serve as a hypothesis-generating process for spatial analysis, producing tentative patterns and relationships that should be confirmed using spatial analytical techniques.
Spatial decision support systems (SDSS) take existing spatial data and use a variety of mathematical models to make projections into the future. This allows urban and regional planners to test intervention decisions prior to implementation.
See also
- General topics
- Cartography
- Complete spatial randomness
- GeoComputation
- Geospatial predictive modeling
- Dimensionally Extended nine-Intersection Model (DE-9IM)
- Geographic information science
- Mathematical statistics
- Modifiable areal unit problem
- Spatial autocorrelation
- Spatial relation
- Specific applications
- Geographic information systems
- Geodemographic segmentation
- Visibility analysis
- Fuzzy architectural spatial analysis
- Suitability analysis
- Extrapolation domain analysis
- Geoinformatics
- Boundary problem (in spatial analysis)
- Spatial epidemiology
- Spatial econometrics
References
- ↑ Mark Monmonier How to Lie with Maps University of Chicago Press, 1996.
- ↑ Knegt, De; Coughenour, M.B.; Skidmore, A.K.; Heitkönig, I.M.A.; Knox, N.M.; Slotow, R.; Prins, H.H.T. (2010). "Spatial autocorrelation and the scaling of species–environment relationships". Ecology. 91: 2455–2465. doi:10.1890/09-1359.1.
- ↑ Ocaña-Riola, R (2010). "Common errors in disease mapping". Geospatial Health. 4 (2): 139–154. doi:10.4081/gh.2010.196. PMID 20503184.
- ↑ Graham J. Upton & Bernard Fingelton: Spatial Data Analysis by Example Volume 1: Point Pattern and Quantitative Data John Wiley & Sons, New York. 1985.
- ↑ Harman H H (1960) Modern Factor Analysis, University of Chicago Press
- ↑ Rummel R J (1970) Applied Factor Analysis. Evanston, ILL: Northwestern University Press.
- ↑ Bell W & E Shevky (1955) Social Area Analysis, Stanford University Press
- ↑ Moser C A & W Scott (1961) British Towns ; A Statistical Study of their Social and Economic Differences, Oliver & Boyd, London.
- ↑ Berry B J & F Horton (1971) Geographic Perspectives on Urban Systems, John Wiley, N-Y.
- ↑ Berry B J & K B Smith eds (1972) City Classification Handbook : Methods and Applications, John Wiley, N-Y.
- ↑ Ciceri M-F (1974) Méthodes d’analyse multivariée dans la géographie anglo-saxonne, Université de Paris-1 ; free download on http://www-ohp.univ-paris1.fr
- ↑ Tucker L R (1964) « The extension of Factor Analysis to three-dimensional matrices », in Frederiksen N & H Gulliksen eds, Contributions to Mathematical Psychology, Holt, Rinehart and Winston, NY.
- ↑ R. Coppi & S. Bolasco, eds. (1989), Multiway data analysis, Elsevier, Amsterdam.
- ↑ Cant, R.G. (1971). "Changes in the location of manufacturing in New Zealand 1957-1968: An application of three-mode factor analysis.". New Zealand Geographer. 27: 38–55. doi:10.1111/j.1745-7939.1971.tb00636.x.
- ↑ Marchand B (1986) The Emergence of Los Angeles, 1940-1970, Pion Ltd, London
- ↑ Wang, JF; Zhang, TL; Fu, BJ (2016). "A measure of spatial stratified heterogeneity". Ecological Indicators. 67: 250–256. doi:10.1016/j.ecolind.2016.02.052.
- ↑ Fotheringham, A. S.; Charlton, M. E.; Brunsdon, C. (1998). "Geographically weighted regression: a natural evolution of the expansion method for spatial data analysis". Environment and Planning A. 30 (11): 1905–1927. doi:10.1068/a301905.
- 1 2 Banerjee, Sudipto; Carlin, Bradley P.; Gelfand, Alan E. (2014), Hierarchical Modeling and Analysis for Spatial Data, Second Edition, Monographs on Statistics and Applied Probability (2nd ed.), Chapman and Hall/CRC, ISBN 9781439819173
- ↑ Banerjee, Sudipto; Gelfand, Alan E.; Finley, Andrew O.; Sang, Huiyan (2008). "Gaussian predictive process models for large spatial datasets". Journal of the Royal Statistical Society Series B. 70 (4): 825–848. doi:10.1111/j.1467-9868.2008.00663.x.
- ↑ Datta, Abhirup; Banerjee, Sudipto; Finley, Andrew O.; Gelfand, Alan E. (2016). "Hierarchical Nearest Neighbor Gaussian Process Models for Large Geostatistical Datasets". Journal of the American Statistical Association. doi:10.1080/01621459.2015.1044091.
- ↑ Honarkhah, M; Caers, J (2010). "Stochastic Simulation of Patterns Using Distance-Based Pattern Modeling". Mathematical Geosciences. 42: 487–517. doi:10.1007/s11004-010-9276-7.
- ↑ Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. (2012). "Multiple-point geostatistical modeling based on the cross-correlation functions" (PDF). Computational Geosciences. 16 (3): 779–79742. doi:10.1007/s10596-012-9287-1.
- ↑ Tahmasebi, P.; Sahimi, M. (2015). "Reconstruction of nonstationary disordered materials and media: Watershed transform and cross-correlation function" (PDF). Physical Review E. 91 (3). doi:10.1103/PhysRevE.91.032401.
- ↑ Tahmasebi, P.; Sahimi, M. (2015). "Geostatistical Simulation and Reconstruction of Porous Media by a Cross-Correlation Function and Integration of Hard and Soft Data" (PDF). Transport in Porous Media. 107 (3): 871–905. doi:10.1007/s11242-015-0471-3.
Further reading
- Abler, R., J. Adams, and P. Gould (1971) Spatial Organization–The Geographer's View of the World, Englewood Cliffs, NJ: Prentice-Hall.
- Anselin, L. (1995) "Local indicators of spatial association – LISA". Geographical Analysis, 27, 93–115.
- Banerjee, Sudipto; Carlin, Bradley P.; Gelfand, Alan E. (2014), Hierarchical Modeling and Analysis for Spatial Data, Second Edition, Monographs on Statistics and Applied Probability (2nd ed.), Chapman and Hall/CRC, ISBN 9781439819173
- Benenson, I. and P. M. Torrens. (2004). Geosimulation: Automata-Based Modeling of Urban Phenomena. Wiley.
- Fotheringham, A. S., C. Brunsdon and M. Charlton (2000) Quantitative Geography: Perspectives on Spatial Data Analysis, Sage.
- Fotheringham, A. S. and M. E. O'Kelly (1989) Spatial Interaction Models: Formulations and Applications, Kluwer Academic
- Fotheringham, A. S.; Rogerson, P. A. (1993). "GIS and spatial analytical problems". International Journal of Geographical Information Systems. 7: 3–19. doi:10.1080/02693799308901936.
- Goodchild, M. F. (1987). "A spatial analytical perspective on geographical information systems" (PDF). International Journal of Geographical Information Systems. 1: 327–44. doi:10.1080/02693798708927820.
- MacEachren, A. M. and D. R. F. Taylor (eds.) (1994) Visualization in Modern Cartography, Pergamon.
- Levine, N. (2010). CrimeStat: A Spatial Statistics Program for the Analysis of Crime Incident Locations. Version 3.3. Ned Levine & Associates, Houston, TX and the National Institute of Justice, Washington, DC. Ch. 1-17 + 2 update chapters
- Miller, H. J. (2004). "Tobler's First Law and spatial analysis". Annals of the Association of American Geographers. 94: 284–289. doi:10.1111/j.1467-8306.2004.09402005.x.
- Miller, H. J. and J. Han (eds.) (2001) Geographic Data Mining and Knowledge Discovery, Taylor and Francis.
- O'Sullivan, D. and D. Unwin (2002) Geographic Information Analysis, Wiley.
- Parker, D. C.; Manson, S. M.; Janssen, M.A.; Hoffmann, M. J.; Deadman, P. (2003). "Multi-agent systems for the simulation of land-use and land-cover change: A review" (PDF). Annals of the Association of American Geographers. 93: 314–337. doi:10.1111/1467-8306.9302004.
- White, R.; Engelen, G. (1997). "Cellular automata as the basis of integrated dynamic regional modelling". Environment and Planning B: Planning and Design. 24: 235–246. doi:10.1068/b240235.
- Scheldeman, X. & van Zonneveld, M. (2010). Training Manual on Spatial Analysis of Plant Diversity and Distribution. Bioversity International.
- Fisher MM, Leung Y (2001) Geocomputational Modelling: techniques and applications. Springer Verlag, Berlin
- Fotheringham, S; Clarke, G; Abrahart, B (1997). "Geocomputation and GIS". Transactions in GIS. 2: 199–200. doi:10.1111/j.1467-9671.1997.tb00010.x.
- Openshaw S and Abrahart RJ (2000) GeoComputation. CRC Press
- Diappi L (2004) Evolving Cities: Geocomputation in Territorial Planning. Ashgate, England
- Longley PA, Brooks SM, McDonnell R, Macmillan B (1998), Geocomputation, a primer. John Wiley and Sons, Chichester
- Ehlen, J; Caldwell, DR; Harding, S (2002). "GeoComputation: what is it?". Comput Environ and Urban Syst. 26: 257–265. doi:10.1016/s0198-9715(01)00047-3.
- Gahegan, M (1999). "What is Geocomputation?". Transaction in GIS. 3: 203–206. doi:10.1111/1467-9671.00017.
- Murgante B., Borruso G., Lapucci A. (2009) "Geocomputation and Urban Planning" Studies in Computational Intelligence, Vol. 176. Springer-Verlag, Berlin.
- Fischer M., Leung Y. (2010) "GeoComputational Modelling: Techniques and Applications" Advances in Spatial Science. Springer-Verlag, Berlin.
- Murgante B., Borruso G., Lapucci A. (2011) "Geocomputation, Sustainability and Environmental Planning" Studies in Computational Intelligence, Vol. 348. Springer-Verlag, Berlin.
- Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. (2012). "Multiple-point geostatistical modeling based on the cross-correlation functions" (PDF). Computational Geosciences. 16 (3): 779–79742. doi:10.1007/s10596-012-9287-1.
- Tóth, G., Kincses, Á., Nagy, Z., (2014) European Spatial Structure LAP LAMBERT Academic Publishing, ISBN 978-3-659-64559-4, doi:10.13140/2.1.1560.2247
External links
- ICA Commission on Geospatial Analysis and Modeling
- An educational resource about spatial statistics and geostatistics
- A comprehensive guide to principles, techniques & software tools
- Social and Spatial Inequalities
- National Center for Geographic Information and Analysis (NCGIA)
- International Cartographic Association (ICA), the world body for mapping and GIScience professionals