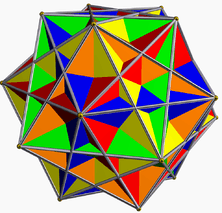
Compound of five cubes
| Compound of five cubes | |
|---|---|
 | |
| Type | Regular compound |
| Coxeter symbol | 2{5,3}[5{4,3}][1] |
| Stellation core | rhombic triacontahedron |
| Convex hull | Dodecahedron |
| Index | UC9 |
| Polyhedra | 5 cubes |
| Faces | 30 squares |
| Edges | 60 |
| Vertices | 20 |
| Dual | Compound of five octahedra |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
The compound of five cubes is one of the five regular polyhedral compounds. This compound was first described by Edmund Hess in 1876.
It is one of five regular compounds, and dual to the compound of five octahedra. It can be seen as a faceting of a regular dodecahedron.
It is one of the stellations of the rhombic triacontahedron. It has icosahedral symmetry (Ih).
Geometry
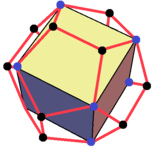
The compound is a faceting of a dodecahedron. Each cube represents one orientation of 8 of 12 vertices within a dodecahedron convex hull.
 |
 |
If the shape is considered as a union of five cubes yielding a simple concave solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182-540+360 = +2.
Edge arrangement
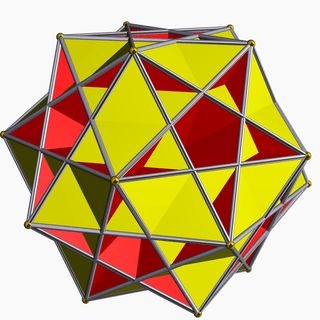
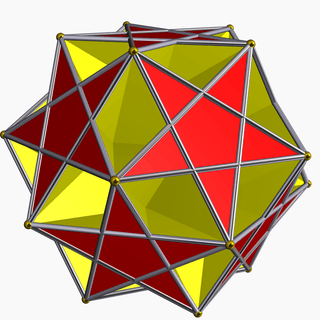
Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron, the great ditrigonal icosidodecahedron, and the ditrigonal dodecadodecahedron.
 Small ditrigonal icosidodecahedron |
 Great ditrigonal icosidodecahedron |
 Ditrigonal dodecadodecahedron |
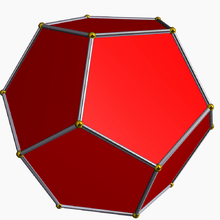 Dodecahedron (convex hull) |
 Compound of five cubes |
 As a spherical tiling |
The compound of ten tetrahedra can be formed by taking each of these five cubes and replacing them with the two tetrahedra of the Stella octangula (which share the same vertex arrangement of a cube).
As a stellation

This compound can be formed as a stellation of the rhombic triacontahedron. The 30 rhombic faces exist in the planes of the 5 cubes.
The stellation facets for construction are:
Other 5-cube compounds
A second 5-cube compound, with octahedral symmetry, also exists. It can be generated by adding a fifth cube to the standard 4-cube compound.

References
- ↑ Regular polytopes, pp.49-50, p.98
- Cromwell, Peter R. (1997), Polyhedra, Cambridge. p 360
- Harman, Michael G. (c. 1974), Polyhedral Compounds, unpublished manuscript.
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
- Cundy, H. and Rollett, A. "Five Cubes in a Dodecahedron." §3.10.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 135–136, 1989.
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
External links
- MathWorld: Cube 5-Compound
- George Hart: Compounds of Cubes
- Steven Dutch: Uniform Polyhedra and Their Duals
- VRML model:
- Klitzing, Richard. "3D compound".
