Nine-point circle
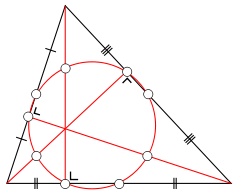

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:
- The midpoint of each side of the triangle
- The foot of each altitude
- The midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).[1][2]
The nine-point circle is also known as Feuerbach's circle, Euler's circle, Terquem's circle, the six-points circle, the twelve-points circle, the n-point circle, the medioscribed circle, the mid circle or the circum-midcircle. Its center is the nine-point center of the triangle.[3][4]
Significant nine points
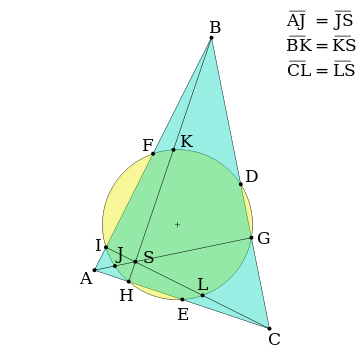
The diagram above shows the nine significant points of the nine-point circle. Points D, E, and F are the midpoints of the three sides of the triangle. Points G, H, and I are the feet of the altitudes of the triangle. Points J, K, and L are the midpoints of the line segments between each altitude's vertex intersection (points A, B, and C) and the triangle's orthocenter (point S).
For an acute triangle, six of the points (the midpoints and altitude feet) lie on the triangle itself; for an obtuse triangle two of the altitudes have feet outside the triangle, but these feet still belong to the nine-point circle.
Discovery
Although he is credited for its discovery, Karl Wilhelm Feuerbach did not entirely discover the nine-point circle, but rather the six point circle, recognizing the significance of the midpoints of the three sides of the triangle and the feet of the altitudes of that triangle. (See Fig. 1, points D, E, F, G, H, and I.) (At a slightly earlier date, Charles Brianchon and Jean-Victor Poncelet had stated and proven the same theorem.) But soon after Feuerbach, mathematician Olry Terquem himself proved the existence of the circle. He was the first to recognize the added significance of the three midpoints between the triangle's vertices and the orthocenter. (See Fig. 1, points J, K, and L.) Thus, Terquem was the first to use the name nine-point circle.
Tangent circles

In 1822 Karl Feuerbach discovered that any triangle's nine-point circle is externally tangent to that triangle's three excircles and internally tangent to its incircle; this result is known as Feuerbach's theorem. He proved that:
- ... the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle... (Feuerbach 1822)
The triangle center at which the incircle and the nine-point circle touch is called the Feuerbach point.
Other properties of the nine-point circle
- The radius of a triangle's circumcircle is twice the radius of that triangle's nine-point circle.[5]:p.153
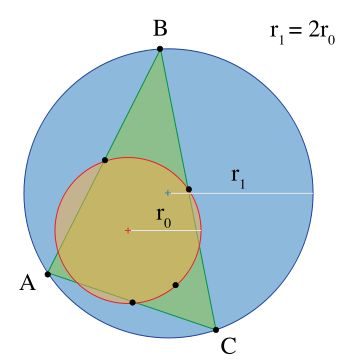 Figure 3
Figure 3
- A nine-point circle bisects a line segment going from the corresponding triangle's orthocenter to any point on its circumcircle.
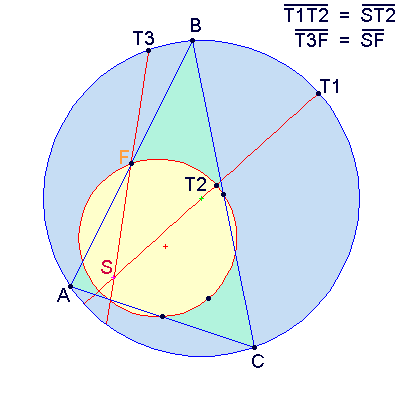 Figure 4
Figure 4
- The center N of the nine-point circle bisects a segment from the orthocenter H to the circumcenter O (making the orthocenter a center of dilation to both circles):[5]:p.152
- ON = NH.
- The nine-point center N is one-fourth of the way along the Euler line from the centroid G to the orthocenter H:[5]:p.153
- HN = 3NG.
- The nine-point circle of a reference triangle is the circumcircle of both the reference triangle's medial triangle (with vertices at the midpoints of the sides of the reference triangle) and its orthic triangle (with vertices at the feet of the reference triangle's altitudes).[5]:p.153
- The center of all rectangular hyperbolas that pass through the vertices of a triangle lies on its nine-point circle. Examples include the well-known rectangular hyperbolas of Keipert, Jeřábek and Feuerbach. This fact is known as the Feuerbach conic theorem.
- If an orthocentric system of four points A, B, C and H is given, then the four triangles formed by any combination of three distinct points of that system all share the same nine-point circle. This is a consequence of symmetry: the sides of one triangle adjacent to a vertex that is an orthocenter to another triangle are segments from that second triangle. A third midpoint lies on their common side. (The same 'midpoints' defining separate nine-point circles, those circles must be concurrent.)
- Consequently, these four triangles have circumcircles with identical radii. Let N represent the common nine-point center and P be an arbitrary point in the plane of the orthocentric system. Then
- NA2+NB2+NC2+NH2 = 3R2
- where R is the common circumradius; and if
- PA2+PB2+PC2+PH2 = K2,
- where K is kept constant, then the locus of P is a circle centered at N with a radius . As P approaches N the locus of P for the corresponding constant K, collapses onto N the nine-point center. Furthermore the nine-point circle is the locus of P such that
- PA2+PB2+PC2+PH2 = 4R2.
- The centers of the incircle and excircles of a triangle form an orthocentric system. The nine-point circle created for that orthocentric system is the circumcircle of the original triangle. The feet of the altitudes in the orthocentric system are the vertices of the original triangle.
- If four arbitrary points A, B, C, D are given that do not form an orthocentric system, then the nine-point circles of ABC, BCD, CDA and DAB concur at a point. The remaining six intersection points of these nine-point circles each concur with the midpoints of the four triangles. Remarkably, there exists a unique nine-point conic, centered at the centroid of these four arbitrary points, that passes through all seven points of intersection of these nine-point circles. Furthermore because of the Feuerbach conic theorem mentioned above, there exists a unique rectangular circumconic, centered at the common intersection point of the four nine-point circles, that passes through the four original arbitrary points as well as the orthocenters of the four triangles.
- If four points A, B, C, D are given that form a cyclic quadrilateral, then the nine-point circles of ABC, BCD, CDA and DAB concur at the anticenter of the cyclic quadrilateral. The nine-point circles are all congruent with a radius of half that of the cyclic quadrilateral's circumcircle. The nine-point circles form a set of four Johnson circles. Consequently the four nine-point centers are cyclic and lie on a circle congruent to the four nine-point circles that is centered at the anticenter of the cyclic quadrilateral. Furthermore the cyclic quadrilateral formed from the four nine-pont centers is homothetic to the reference cyclic quadrilateral ABCD by a factor of −1/2 and its homothetic center (N) lies on the line connecting the circumcenter (O) to the anticenter (M) where
- ON = 2NM.
- The orthopole of lines passing through the circumcenter lie on the nine-point circle.
- A triangle's circumcircle, its nine-point circle, its polar circle, and the circumcircle of its tangential triangle[6] are coaxal.[7]
- Trilinear coordinates for the center of the Kiepert hyperbola are
- (b2 − c2)2/a : (c2 − a2)2/b : (a2 − b2)2/c
- Trilinear coordinates for the center of the Jeřábek hyperbola are
- cos A sin2(B − C) : cos B sin2(C − A) : cos C sin2(A − B)
- Letting x : y : z be a variable point in trilinear coordinates, an equation for the nine-point circle is
- x2sin 2A + y2sin 2B + z2sin 2C − 2(yz sin A + zx sin B + xy sin C) = 0.
Generalization
The circle is an instance of a conic section and the nine-point circle is an instance of the general nine-point conic that has been constructed with relation to a triangle ABC and a fourth point P, where the particular nine-point circle instance arises when P is the orthocenter of ABC. The vertices of the triangle and P determine a complete quadrilateral and three "diagonal points" where opposite sides of the quadrilateral intersect. There are six "sidelines" in the quadrilateral; the nine-point conic intersects the midpoints of these and also includes the diagonal points. The conic is an ellipse when P is interior to ABC or in a region sharing vertical angles with the triangle, but a nine-point hyperbola occurs when P is in one of the three adjacent regions, and the hyperbola is rectangular when P lies on the circumcircle of ABC.
See also
Notes
- ↑ Altshiller-Court (1925, pp. 103–110)
- ↑ Kay (1969, pp. 18,245)
- ↑ Kocik, Jerzy; Solecki, Andrzej (2009). "Disentangling a Triangle". Amer. Math. Monthly. 116 (3): 228–237. doi:10.4169/193009709x470065. Kocik and Solecki (sharers of a 2010 Lester R. Ford Award) give a proof of the Nine-Point Circle Theorem.
- ↑ Casey, John (1886). Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (4th ed.). London: Longmans, Green, & Co. p. 58.
- 1 2 3 4 Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
- ↑ Altshiller-Court (1925, p. 98)
- ↑ Altshiller-Court (1925, p. 241)
References
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52013504
- Feuerbach, Karl Wilhelm; Buzengeiger, Carl Heribert Ignatz (1822), Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figuren. Eine analytisch-trigonometrische Abhandlung (Monograph ed.), Nürnberg: Wiessner.
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69012075
External links
- "A Javascript demonstration of the nine point circle" at rykap.com
- Encyclopedia of Triangles Centers by Clark Kimberling. The nine-point center is indexed as X(5), the Feuerbach point, as X(11), the center of the Kiepert hyperbola as X(115), and the center of the Jeřábek hyperbola as X(125).
- History about the nine-point circle based on J.S. MacKay's article from 1892: History of the Nine Point Circle
- Weisstein, Eric W. "Nine-Point Circle". MathWorld.
- Nine Point Circle in Java at cut-the-knot
- Feuerbach's Theorem: a Proof at cut-the-knot
- Special lines and circles in a triangle by Walter Fendt (requires Java)
- An interactive Java applet showing several triangle centers that lies on the Nine Point Circle.
- Interactive Nine Point Circle applet from the Wolfram Demonstrations Project
- Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.