Circumconic and inconic
In triangle geometry, a circumconic is a conic section that passes through the three vertices of a triangle,[1] and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.[2]
Suppose A,B,C are distinct non-collinear points, and let ΔABC denote the triangle whose vertices are A,B,C. Following common practice, A denotes not only the vertex but also the angle BAC at vertex A, and similarly for B and C as angles in ΔABC. Let a = |BC|, b = |CA|, c = |AB|, the sidelengths of ΔABC.
In trilinear coordinates, the general circumconic is the locus of a variable point X = x : y : z satisfying an equation
- uyz + vzx + wxy = 0,
for some point u : v : w. The isogonal conjugate of each point X on the circumconic, other than A,B,C, is a point on the line
- ux + vy + wz = 0.
This line meets the circumcircle of ΔABC in 0,1, or 2 points according as the circumconic is an ellipse, parabola, or hyperbola.
The general inconic is tangent to the three sidelines of ΔABC and is given by the equation
- u2x2 + v2y2 + w2z2 − 2vwyz − 2wuzx − 2uvxy = 0.
Centers and tangent lines
Circumconic
The center of the general circumconic is the point
- u(−au + bv + cw) : v(au − bv + cw) : w(au + bv − cw).
The lines tangent to the general circumconic at the vertices A,B,C are, respectively,
- wv + vz = 0,
- uz + wx = 0,
- vx + uy = 0.
Inconic
The center of the general inconic is the point
- cy + bz : az + cx : bx + ay.
The lines tangent to the general inconic are the sidelines of ΔABC, given by the equations x = 0, y = 0, z = 0.
Other features
Circumconic
- Each noncircular circumconic meets the circumcircle of ΔABC in a point other than A, B, and C, often called the fourth point of intersection, given by trilinear coordinates
- (cx − az)(ay − bx) : (ay − bx)(bz − cy) : (bz − cy)(cx − az)
- If P = p : q : r is a point on the general circumconic, then the line tangent to the conic at P is given by
- (vr + wq)x + (wp + ur)y + (uq + vp)z = 0.
- The general circumconic reduces to a parabola if and only if
- u2a2 + v2b2 + w2c2 − 2vwbc − 2wuca − 2uvab = 0,
- and to a rectangular hyperbola if and only if
- u cos A + v cos B + w cos C = 0.
- Of all triangles inscribed in a given ellipse, the centroid of the one with greatest area coincides with the center of the ellipse.[3]:p.147 The given ellipse, going through this triangle's three vertices and centered at the triangle's centroid, is called the triangle's Steiner circumellipse.
Inconic
- The general inconic reduces to a parabola if and only if
- ubc + vca + wab = 0,
- in which case it is tangent externally to one of the sides of the triangle and is tangent to the extensions of the other two sides.
- Suppose that p1 : q1 : r1 and p2 : q2 : r2 are distinct points, and let
- X = (p1 + p2t) : (q1 + q2t) : (r1 + r2t).
- As the parameter t ranges through the real numbers, the locus of X is a line. Define
- X2 = (p1 + p2t)2 : (q1 + q2t)2 : (r1 + r2t)2.
- The locus of X2 is the inconic, necessarily an ellipse, given by the equation
- L4x2 + M4y2 + N4z2 − 2M2N2yz − 2N2L2zx − 2L2M2xy = 0,
- where
- L = q1r2 − r1q2,
- M = r1p2 − p1r2,
- N = p1q2 − q1p2.
- A point in the interior of a triangle is the center of an inellipse of the triangle if and only if the point lies in the interior of the triangle whose vertices lie at the midpoints of the original triangle's sides.[3]:p.139 For a given point inside that medial triangle, the inellipse with its center at that point is unique.[3]:p.142
- The inellipse with the largest area is the Steiner inellipse, also called the midpoint inellipse, with its center at the triangle's centroid.[3]:p.145 In general, the ratio of the inellipse's area to the triangle's area, in terms of the unit-sum barycentric coordinates
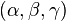 of the inellipse's center, is[3]:p.143
of the inellipse's center, is[3]:p.143
- which is maximized by the centroid's barycentric coordinates
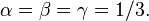
- The lines connecting the tangency points of any inellipse of a triangle with the opposite vertices of the triangle are concurrent.[3]:p.148
Extension to quadrilaterals
All the centers of inellipses of a given quadrilateral fall on the line segment connecting the midpoints of the diagonals of the quadrilateral.[3]:p.136
Examples
- Circumconics
- Circumcircle, the unique circle that passes through a triangle's three vertices
- Steiner circumellipse, the unique ellipse that passes through a triangle's three vertices and is centered at the triangle's centroid
- Kiepert hyperbola, the unique conic which passes through a triangle's three vertices, its centroid, and its orthocenter
- Jeřábek hyperbola, a rectangular hyperbola centered on a triangle's nine-point circle and passing through the triangle's three vertices as well as its circumcenter, orthocenter, and various other notable centers
- Feuerbach hyperbola, a rectangular hyperbola that passes through a triangle's orthocenter, Nagel point, and various other notable points, and has center on the nine-point circle.
- Inconics
- Incircle, the unique circle that is internally tangent to a triangle's three sides
- Steiner inellipse, the unique ellipse that is tangent to a triangle's three sides at their midpoints
- Mandart inellipse, the unique ellipse tangent to a triangle's sides at the contact points of its excircles
- Kiepert parabola
- Yff parabola
References
- ↑ Weisstein, Eric W. "Circumconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Circumconic.html
- ↑ Weisstein, Eric W. "Inconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Inconic.htm
- 1 2 3 4 5 6 7 Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979.
External links
- Circumconic at MathWorld
- Inconic at MathWorld