Regular skew polyhedron

In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.[1]

Infinite regular skew polyhedra that span 3-space or higher are called regular skew apeirohedra.

History

According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to regular skew polyhedra.

Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes.

The regular skew polyhedra, represented by {l,m|n}, follow this equation:

2*sin(π/l)*sin(π/m)=cos(π/n)

A first set {l, m | n}, repeats the five convex Platonic solids, and one nonconvex Kepler-Poinsot solid:

{l, m | n} Faces Edges Vertices p Polyhedron Symmetry
order
{3,3| 3} = {3,3} 464 0 Tetrahedron12
{3,4| 4} = {3,4} 8126 0 Octahedron24
{4,3| 4} = {4,3} 6128 0 Cube24
{3,5| 5} = {3,5} 203012 0Icosahedron60
{5,3| 5} = {5,3} 123020 0 Dodecahedron60
{5,5| 3} = {5,5/2} 123012 4 Great dodecahedron60

Finite regular skew polyhedra of 4-space

A4 Coxeter plane projections
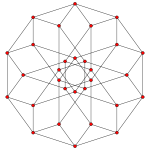{4, 6 | 3} {6, 4 | 3}
Runcinated 5-cell
(20 vertices, 60 edges)		 Bitruncated 5-cell
(30 vertices, 60 edges)
F4 Coxeter plane projections
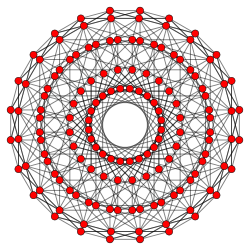{4, 8 | 3} {8, 4 | 3}
Runcinated 24-cell
(144 vertices, 576 edges)		 Bitruncated 24-cell
(288 vertices, 576 edges)
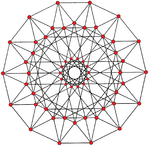{3,8|,4} = {3,8}8 {4,6|,3} = {4,6}6
42 vertices, 168 edges 56 vertices, 168 edges
Some of the 4-dimensional regular skew polyhedra fits inside the uniform polychora as shown in the top 4 projections.

Coxeter also enumerated the a larger set of finite regular polyhedra in his paper "regular skew polyhedra in three and four dimensions, and their topological analogues".

Just like the infinite skew polyhedra represent manifold surfaces between the cells of the convex uniform honeycombs, the finite forms all represent manifold surfaces within the cells of the uniform polychora.

Polyhedra of the form {2p, 2q | r} are related to Coxeter group symmetry of [(p,r,q,r)], which reduces to the linear [r,p,r] when q is 2. Coxeter gives these symmetry as [[(p,r,q,r)]+] which he says is isomorphic to his abstract group (2p,2q|2,r). The related honeycomb has the extended symmetry [[(p,r,q,r)]].[2]

{2p,4|r} is represented by the {2p} faces of the bitruncated {r,p,r} uniform 4-polytope, and {4,2p|r} is represented by square faces of the runcinated {r,p,r}.

{4,4|n} produces a n-n duoprism, and specifically {4,4|4} fits inside of a {4}x{4} tesseract.

The {4,4| n} solutions represent the square faces of the duoprisms, with the n-gonal faces as holes and represent a clifford torus, and an approximation of a duocylinder
{4,4|6} has 36 square faces, seen in perspective projection as squares extracted from a 6,6 duoprism.
A ring of 60 triangles make a regular skew polyhedron within a subset of faces of a 600-cell.
Even ordered solutions
{l, m | n} Faces Edges Vertices p Structure Symmetry Order Related uniform polychora
{4,4| 3} 91891D3xD3[[3,2,3]+]93-3 duoprism
{4,4| 4} 1632161D4xD4[[4,2,4]+]164-4 duoprism or tesseract
{4,4| 5} 2550251D5xD5[[5,2,5]+]255-5 duoprism
{4,4| 6} 3672361D6xD6[[6,2,6]+]366-6 duoprism
{4,4| n} n22n2n21DnxDn[[n,2,n]+]n2n-n duoprism
{4,6| 3} 3060206S5[[3,3,3]+]60Runcinated 5-cell
{6,4| 3} 2060306S5[[3,3,3]+]60Bitruncated 5-cell
{4,8| 3} 28857614473[[3,4,3]+]576Runcinated 24-cell
{8,4| 3} 14457628873[[3,4,3]+]576Bitruncated 24-cell
pentagrammic solutions
{l, m | n} Faces Edges Vertices p Structure Symmetry Order Related uniform polychora
{4,5| 5} 901807210A6[[5/2,5,5/2]+]360Runcinated grand stellated 120-cell
{5,4| 5} 721809010A6[[5/2,5,5/2]+]360Bitruncated grand stellated 120-cell
{l, m | n} Faces Edges Vertices p Structure Order
{4,5| 4} 4080325?160
{5,4| 4} 3280405?160
{4,7| 3} 42842410LF(2,7)168
{7,4| 3} 24844210LF(2,7)168
{5,5| 4} 721807219 A6360
{6,7| 3} 182546156105LF(2,13)1092
{7,6| 3} 156546182105LF(2,13)1092
{7,7| 3} 156546156118LF(2,13)1092
{4,9| 3} 6121224272171LF(2,17)2448
{9,4| 3} 2721224612171LF(2,17)2448
{7,8| 3} 1536537613441249?10752
{8,7| 3} 1344537615361249?10752

A final set is based on Coxeter's further extended form {q1,m|q2,q3...} or with q2 unspecified: {l, m |, q}. These can also be represented a regular finite map or {l, m}2q, and group Gl,m,q.[3]

{l, m |, q} or {l, m}2q Faces Edges Vertices p Structure Order Notes
{3,6|,q} = {3,6}2q 2q23q2q21G3,6,2q2q2
{3,2q|,3} = {3,2q}6 2q23q23q(q-1)*(q-2)/2G3,6,2q2q2
{3,7|,4} = {3,7}8 5684243LF(2,7)168
{3,8|,4} = {3,8}8 112168428PGL(2,7)336Related to complex polyhedron (1 1 114)4,
{4,6|,3} = {4,6}6 841685615PGL(2,7)336Related to complex polyhedron (14 14 11)(3),
{3,7|,6} = {3,7}12 36454615614LF(2,13)1092
{3,7|,7} = {3,7}14 36454615614LF(2,13)1092
{3,8|,5} = {3,8}10 720108027046G3,8,102160Related to complex polyhedron (1 1 114)5,
{3,10|,4} = {3,10}8 720108021673G3,8,102160Related to complex polyhedron (1 1 115)4,
{4,6|,2} = {4,6}4 122483S4×S248
{5,6|,2} = {5,6}4 2460209A5×S2120
{3,11|,4} = {3,11}8 20243036552231LF(2,23)6072
{3,7|,8} = {3,7}16 358453761536129G3,7,1710752
{3,9|,5} = {3,9}10 121801827040601016LF(2,29)×A336540

See also

Notes

  1. ↑ Abstract regular polytopes, p.7, p.17
  2. ↑ Coxeter, Regular and Semi-Regular Polytopes II 2.34)
  3. ↑ Coxeter and Moser, Generators and relations for discrete groups, Sec 8.6 Maps having specified Petrie polygons. p. 110

References

This article is issued from Wikipedia - version of the 11/26/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.