Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.[1] Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”[2]

The theorem appears in a 1922 paper of Ernst Steinitz, after whom it is named. It can be proven by mathematical induction (as Steinitz did), by finding the minimum-energy state of a two-dimensional spring system into three dimensions, or by using the circle packing theorem. Several extensions of the theorem are known, in which the polyhedron that realizes a given graph has additional constraints; for instance, every polyhedral graph is the graph of a convex polyhedron with integer coordinates, or the graph of a convex polyhedron all of whose edges are tangent to a common midsphere.

In higher dimensions, the problem of characterizing the graphs of convex polytopes remains open.

Definitions and statement of the theorem

Illuminating the skeleton of a convex polyhedron from a light source close to one of its faces causes its shadows to form a planar Schlegel diagram.

An undirected graph is a system of vertices and edges, each edge connecting two of the vertices. From any polyhedron one can form a graph, by letting the vertices of the graph correspond to the vertices of the polyhedron and by connecting any two graph vertices by an edge whenever the corresponding two polyhedron vertices are the endpoints of an edge of the polyhedron. This graph is known as the skeleton of the polyhedron.

A graph is planar if it can be drawn with its vertices as points in the Euclidean plane, and its edges as curves that connect these points, such that no two edge curves cross each other and such that the point representing a vertex lies on the curve representing an edge only when the vertex is an endpoint of the edge. By Fáry's theorem, it is sufficient to consider only planar drawings in which the curves representing the edges are line segments. A graph is 3-connected if, after the removal of any two of its vertices, any other pair of vertices remain connected by a path. Steinitz's theorem states that these two conditions are both necessary and sufficient to characterize the skeletons of three-dimensional convex polyhedra: a given graph G is the graph of a convex three-dimensional polyhedron, if and only if G is planar and 3-vertex-connected.[3][2]

History and naming

Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916.[4]

The name "Steinitz's theorem" has also been applied to other results of Steinitz:

Proofs

One direction of Steinitz's theorem (the easier direction to prove) states that the graph of every convex polyhedron is planar and 3-connected. As shown in the illustration, planarity can be shown by using a Schlegel diagram: if one places a light source near one face of the polyhedron, and a plane on the other side, the shadows of the polyhedron edges will form a planar graph, embedded in such a way that the edges are straight line segments. The 3-connectivity of a polyhedral graph is a special case of Balinski's theorem that the graph of any k-dimensional convex polytope is k-connected.[11]

The other, more difficult, direction of Steinitz's theorem states that every planar 3-connected graph is the graph of a convex polyhedron. There are three standard approaches for this part: proofs by induction, lifting two-dimensional Tutte embeddings into three dimensions using the Maxwell–Cremona correspondence, and methods using the circle packing theorem to generate a canonical polyhedron.

Induction

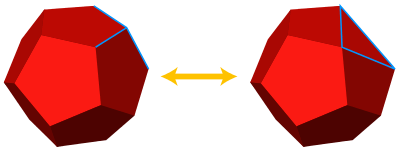
Δ-Y and Y-Δ transforms of a polyhedron

Steinitz' original proof involved finding a sequence of Δ-Y and Y-Δ transforms that reduce any 3-connected planar graph to K4, the graph of the tetrahedron. A Y-Δ transform removes a degree-three vertex from a graph, adding edges between all of its former neighbors if those edges did not already exist; the reverse transformation, a Δ-Y transform, removes the edges of a triangle from a graph and replaces them by a new degree-three vertex adjacent to the same three vertices. Once such a sequence is found, it can be reversed to give a sequence of Δ-Y and Y-Δ transforms that build up the desired polyhedron step by step starting from a polyhedron. Each Y-Δ transform transform in this sequence can be performed by slicing off a degree-three vertex from a polyhedron. A Δ-Y transform can be performed by removing a triangular face from a polyhedron and extending its neighboring faces until the point where they meet, but only when that triple intersection point of the three neighboring faces is on the correct side of the polyhedron; when the triple intersection point is not on the correct side, a projective transformation of the polyhedron suffices to move it to the correct side. Therefore, by induction on the number of Δ-Y and Y-Δ transforms needed to reduce a given graph to K4, every polyhedral graph can be realized as a polyhedron.[4]

A later work by Epifanov strengthened Steinitz's proof that every polyhedral graph can be reduced to K4 by Δ-Y and Y-Δ transforms. Epifanov proved that if two vertices are specified in a planar graph, then the graph can be reduced to a single edge between those terminals by combining Δ-Y and Y-Δ transforms with series-parallel reductions.[12] Epifanov's proof was complicated and non-constructive, but it was simplified by Truemper using methods based on graph minors. Truemper observed that every grid graph is reducible by Δ-Y and Y-Δ transforms in this way, that this reducibility is preserved by graph minors, and that every planar graph is a minor of a grid graph.[13] This idea can be used to replace Steinitz's lemma that a reduction sequence exists, in a proof of Steinitz's theorem using induction in the same way.[3] However, there exist graphs that require a nonlinear number of steps in any sequence of Δ-Y and Y-Δ transforms. More precisely, Ω(n3/2) steps are sometimes necessary, and the best known upper bound on the number of steps is even worse, O(n2).[14]

An alternative form of induction proof is based on removing edges (and compressing out the degree-two vertices that might be performed by this removal) or contracting edges and forming a minor of the given planar graph. Any polyhedral graph can be reduced to K4 by a linear number of these operations, and again the operations can be reversed and the reversed operations performed geometrically, giving a polyhedral realization of the graph. However, while it is simpler to prove that a reduction sequence exists for this type of argument, and the reduction sequences are shorter, the geometric steps needed to reverse the sequence are more complicated.[15]

Lifting

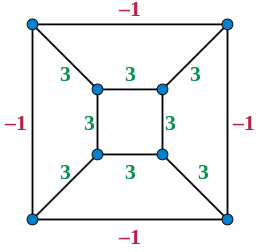
An equilibrium stress on the graph of a cube, corresponding to a lift of this drawing to a three-dimensional frustum

If a graph is drawn in the plane with straight line edges, then an equilibrium stress is defined as an assignment of nonzero real numbers (weights) to the edges, with the property that each vertex is in the position given by the weighted sum of its neighbors. According to the Maxwell–Cremona correspondence, an equilibrium stress can be lifted to a piecewise linear continuous three-dimensional surface such that the edges forming the boundaries between the flat parts of the surface project to the given drawing. The weight and length of each edge determines the difference in slopes of the surface on either side of the edge, and the condition that each vertex is in equilibrium with its neighbors is equivalent to the condition that these slope differences cause the surface to meet up with itself correctly in the neighborhood of the vertex. Positive weights translate to convex dihedral angles between two faces of the piecewise linear surface, and negative weights translate to concave dihedral angles. Conversely, every continuous piecewise-linear surface comes from an equilibrium stress in this way. If a finite planar graph is drawn and given an equilibrium stress in such a way that all interior edges of the drawing have positive weights, and all exterior edges have negative weights, then by translating this stress into a three-dimensional surface in this way, and then replacing the flat surface representing the exterior of the graph by its complement in the same plane, one obtains a convex poyhedron, with the additional property that its perpendicular projection onto the plane has no crossings.[16][17]

The Maxwell–Cremona correspondence has been used to obtain polyhedral realizations of polyhedral graphs by combining it with a planar graph drawing method of W. T. Tutte, the Tutte embedding. Tutte's method begins by fixing one face of a polyhedral graph into convex position in the plane. This face will become the outer face of a drawing of a graph. The method continues by setting up a system of linear equations in the vertex coordinates, according to which each remaining vertex should be placed at the average of its neighbors. Then as Tutte showed, this system of equations will have a unique solution in which each face of the graph is drawn as a convex polygon.[18] The result is almost an equilibrium stress: if one assigns weight one to each interior edge, then each interior vertex of the drawing is in equilibrium. However, it is not always possible to assign negative numbers to the exterior edges so that they, too, are in equilibrium. Such an assignment is always possible when the outer face is a triangle, and so this method can be used to realize any polyhedral graph that has a triangular face. If a polyhedral graph does not contain a triangular face, its dual graph does contain a triangle and is also polyhedral, so one can realize the dual in this way and then realize the original graph as the polar polyhedron of the dual realization.[19][20] It is also possible to realize any polyhedral graph directly by choosing the outer face to be any face with at most five vertices (something that exists in all polyhedral graphs) and choosing more carefully the fixed shape of this face in such a way that the Tutte embedding can be lifted,[21] or by using an incremental method instead of Tutte's method to find a liftable planar drawing that does not have equal weights for all the interior edges.[22]

Circle packing

A polyhedron realized from a circle packing. The circles representing the vertices of the polyhedron are their horizons on the sphere, and the circles representing the faces (dual vertices) are the intersections of the sphere with the face planes.

According to one variant of the circle packing theorem, for every polyhedral graph and its dual graph, there exists a system of circles in the plane or on any sphere, representing the vertices of both graphs, so that two adjacent vertices in the same graph are represented by tangent circles, a primal and dual vertex that represent a vertex and face that touch each other are represented by orthogonal circles, and all remaining pairs of circles are disjoint.[23] From such a representation on a sphere, one can find a polyhedral realization of the given graph as the intersection of a collection of halfspaces, one for each circle that represents a dual vertex, with the boundary of the halfspace containing the circle. Alternatively and equivalently, one can find the same polyhedron as the convex hull of a collection of points (its vertices), such that the horizon seen when viewing the sphere from any vertex equals the circle that corresponds to that vertex. The sphere becomes the midsphere of the realization: each edge of the polyhedron is tangent to it, at the point where two tangent primal circles and two dual circles orthogonal to the primal circles and tangent to each other all meet.[24]

Realizations with additional properties

Integer coordinates

It is possible to prove a stronger form of Steinitz's theorem, that any polyhedral graph can be realized by a convex polyhedron for which all of the vertex coordinates are integers. The integers resulting from induction-based proofs (including Steinitz's original proof) are doubly exponential in the number of vertices of the given polyhedral graph; that is, writing them down would require an exponential number of bits.[25] However, subsequent researchers have found lifting-based realization algorithms that use only O(n) bits per vertex.[21][26] It is also possible to relax the requirement that the coordinates be integers, and assign coordinates in such a way that the x-coordinates of the vertices are distinct integers in the range [0,2n − 4] and the other two coordinates are real numbers in the range [0,1], so that each edge has length at least one while the overall polyhedron has volume O(n).[27] Some polyhedral graphs are known to be realizable on grids of only polynomial size; in particular this is true for the pyramids (realizations of wheel graphs), prisms (realizations of prism graphs), and stacked polyhedra (realizations of Apollonian networks).[28]

Equal slopes

A Halin graph is a planar graph formed from a planar-embedded tree (with no degree-two vertices) by connecting the leaves of the tree into a cycle. Every Halin graph can be realized by a polyhedron in which this cycle forms a horizontal base face, every other face lies directly above the base face (as in the polyhedra realized through lifting), and every face has the same slope. Equivalently, the straight skeleton of the base face is combinatorially equivalent to the tree from which the Halin graph was formed. The proof of this result uses induction: any rooted tree may reduced to a smaller tree by removing the leaves from an internal node whose children are all leaves, the Halin graph formed from the smaller tree has a realization by the induction hypothesis, and it is possible to modify this realization in order to add any number of leaf children to the tree node whose children were removed.[29]

Specifying the shape of a face

In any polyhedron that represents a given polyhedral graph G, the faces of G are exactly the cycles in G that do not separate G into two components: that is, removing a facial cycle from G leaves the rest of G as a connected subgraph. Thus, the faces are uniquely determined from the graph structure. Another strengthening of Steinitz's theorem, by Barnette and Grünbaum, states that for any polyhedral graph, any face of the graph, and any convex polygon representing that face, it is possible to find a polyhedral realization of the whole graph that has the specified shape for the designated face. This is related to a theorem of Tutte, that any polyhedral graph can be drawn in the plane with all faces convex and any specified shape for its outer face. However, the planar graph drawings produced by Tutte's method do not necessarily lift to convex polyhedra. Instead, Barnette and Grünbaum prove this result using an inductive method[30] It is also always possible, given a polyhedral graph G and an arbitrary cycle C, to find a realization such that C forms the silhouette of the realization under parallel projection.[31]

Tangent spheres

The Koebe–Andreev–Thurston circle packing theorem can be interpreted as providing another strengthening of Steinitz's theorem, that every 3-connected planar graph may be represented as a convex polyhedron in such a way that all of its edges are tangent to the same unit sphere.[24] By performing a carefully chosen Möbius transformation of a circle packing before transforming it into a polyhedron, it is possible to find a polyhedral realization that realizes all the symmetries of the underlying graph, in the sense that every graph automorphism is a symmetry of the polyhedral realization.[32][33] More generally, if G is a polyhedral graph and K is any smooth three-dimensional convex body, it is possible to find a polyhedral representation of G in which all edges are tangent to K.[34]

Circle packing methods can also be used to characterize the graphs of polyhedra that have a circumsphere or insphere. The characterization involves edge weights, constrained by systems of linear inequalities. These weights correspond to the angles made by adjacent circles in a system of circles, made by the intersections of the faces of the polyhedron with their circumsphere or the horizons of the vertices of the polyhedron on its insphere.[35][36]

Related results

The Szilassi polyhedron, a non-convex polyhedral realization of the Heawood graph with the topology of a torus

In any dimension higher than three, the algorithmic Steinitz problem (given a lattice, determine whether it is the face lattice of a convex polytope) is complete for the existential theory of the reals by Richter-Gebert's universality theorem.[37] However, because a given graph may correspond to more than one face lattice, it is difficult to extend this completeness result to the problem of recognizing the graphs of 4-polytopes, and this problem's complexity remains open.

Researchers have also found graph-theoretic characterizations of the graphs of certain special classes of three-dimensional non-convex polyhedra[38][39] and four-dimensional convex polytopes.[40][41][42] However, in both cases, the general problem remains unsolved. Indeed, even the problem of determining which complete graphs are the graphs of non-convex polyhedra (other than K4 for the tetrahedron and K7 for the Császár polyhedron) remains unsolved.[43]

László Lovász has shown a correspondence between polyhedral representations of graphs and matrices realizing the Colin de Verdière graph invariants of the same graphs.[44]

References

  1. ↑ Weisstein, Eric W. "Polyhedral graph". MathWorld.
  2. 1 2 Branko Grünbaum, Convex Polytopes, 2nd edition, prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler, 2003, ISBN 0-387-40409-0, ISBN 978-0-387-40409-7, 466pp.
  3. 1 2 Lectures on Polytopes, by Günter M. Ziegler (1995) ISBN 0-387-94365-X , Chapter 4 "Steinitz' Theorem for 3-Polytopes", p.103.
  4. 1 2 Steinitz, Ernst (1922), "Polyeder und Raumeinteilungen", Encyclopädie der mathematischen Wissenschaften, Band 3 (Geometries) (IIIAB12), pp. 1–139, Abgeschlossen am 31. August 1916.
  5. ↑ Zynel, Mariusz (1996), "The Steinitz theorem and the dimension of a vector space", Formalized Mathematics, 5 (8): 423–428, CiteSeerX 10.1.1.79.1707Freely accessible.
  6. ↑ Kirkpatrick, David; Mishra, Bhubaneswar; Yap, Chee-Keng (1992), "Quantitative Steinitz's theorems with applications to multifingered grasping", Discrete & Computational Geometry, 7 (1): 295–318, doi:10.1007/BF02187843.
  7. ↑ Rosenthal, Peter (1987), "The remarkable theorem of Lévy and Steinitz", American Mathematical Monthly, 94 (4): 342–351, doi:10.2307/2323094, JSTOR 2323094.
  8. ↑ Banaszczyk, Wojciech (1991). "Chapter 3.10 The Lévy-Steinitz theorem". Additive subgroups of topological vector spaces. Lecture Notes inMathematics. 1466. Berlin: Springer-Verlag. pp. viii+178. ISBN 3-540-53917-4. MR 1119302.
  9. ↑ Kadets, V. M.; Kadets, M. I. (1991). "Chapter 6 The Steinitz theorem and B-convexity". Rearrangements of series in Banach spaces. Translations of Mathematical Monographs. 86 (Translated by Harold H. McFaden from the Russian-language (Tartu) 1988 ed.). Providence, RI: American Mathematical Society. pp. iv+123. ISBN 0-8218-4546-2. MR 1108619.
  10. ↑ Kadets, Mikhail I.; Kadets, Vladimir M. (1997). "Chapter 2.1 Steinitz's theorem on the sum range of a series, Chapter 7 The Steinitz theorem and B-convexity". Series in Banach spaces: Conditional and unconditional convergence. Operator Theory: Advances and Applications. 94 (Translated by Andrei Iacob from the Russian-language ed.). Basel: Birkhäuser Verlag. pp. viii+156. ISBN 3-7643-5401-1. MR 1442255.
  11. ↑ Balinski, M. L. (1961), "On the graph structure of convex polyhedra in n-space", Pacific Journal of Mathematics, 11 (2): 431–434, doi:10.2140/pjm.1961.11.431, MR 0126765.
  12. ↑ Epifanov, G. V. (1966), "Reduction of a plane graph to an edge by star-triangle transformations", Dokl. Akad. Nauk SSSR, 166: 19–22, MR 0201337.
  13. ↑ Truemper, K. (1989), "On the delta-wye reduction for planar graphs", J. Graph Theory, 13 (2): 141–148, doi:10.1002/jgt.3190130202, MR 994737.
  14. ↑ Chang, Hsien-Chih; Erickson, Jeff (September 27, 2015), Electrical reduction, homotopy moves, and defect.
  15. ↑ Barnette, David W.; Grünbaum, Branko (1969), "On Steinitz's theorem concerning convex 3-polytopes and on some properties of planar graphs", The Many Facets of Graph Theory (Proc. Conf., Western Mich. Univ., Kalamazoo, Mich., 1968), Springer, pp. 27–40, MR 0250916.
  16. ↑ Maxwell, J. Clerk (1864), "On reciprocal figures and diagrams of forces", Philosophical Magazine (4th Ser.), 27: 250–261.
  17. ↑ Whiteley, Walter (1982), "Motions and stresses of projected polyhedra", Structural Topology, 7: 13–38, MR 721947.
  18. ↑ Tutte, W. T. (1963), "How to draw a graph", Proceedings of the London Mathematical Society, 13: 743–767, doi:10.1112/plms/s3-13.1.743, MR 0158387.
  19. ↑ Onn, Shmuel; Sturmfels, Bernd (1994), "A quantitative Steinitz' theorem", Beiträge Algebra Geom., 35 (1): 125–129, MR 1287206.
  20. ↑ Eades, Peter; Garvan, Patrick (1996), "Drawing stressed planar graphs in three dimensions", Graph Drawing (GD '95), Lecture Notes in Computer Science, 1027, Springer, pp. 212–223, doi:10.1007/bfb0021805.
  21. 1 2 Ribó Mor, Ares; Rote, Günter; Schulz, André (2011), "Small Grid Embeddings of 3-Polytopes", Discrete & Computational Geometry, 45 (1): 65–87, doi:10.1007/s00454-010-9301-0.
  22. ↑ Chrobak, Marek; Goodrich, Michael T.; Tamassia, Roberto (1996), "Convex drawings of graphs in two and three dimensions", Proceedings of the 12th ACM Symposium on Computational Geometry (SoCG '96), ACM, pp. 319–328, doi:10.1145/237218.237401.
  23. ↑ Brightwell, Graham R.; Scheinerman, Edward R. (1993), "Representations of planar graphs", SIAM J. Discrete Math., 6 (2): 214–229, doi:10.1137/0406017.
  24. 1 2 Ziegler, Günter M. (2007), "Convex polytopes: extremal constructions and f-vector shapes. Section 1.3: Steinitz's theorem via circle packings", in Miller, Ezra; Reiner, Victor; Sturmfels, Bernd, Geometric Combinatorics, IAS/Park City Mathematics Series, 13, American Mathematical Society, pp. 628–642, ISBN 978-0-8218-3736-8.
  25. ↑ Venkatasubramanian, Suresh (2006), Planar graphs and Steinitz's theorem.
  26. ↑ Buchin, Kevin; Schulz, André (2010), "On the number of spanning trees a planar graph can have", Algorithms - 18th Annual European Symposium (ESA 2010), Lecture Notes in Computer Science, 6346, Springer-Verlag, pp. 110–121, doi:10.1007/978-3-642-15775-2.
  27. ↑ Schulz, André (2011), "Drawing 3-polytopes with good vertex resolution" (PDF), Journal of Graph Algorithms and Applications, 15 (1): 33–52, doi:10.7155/jgaa.00216.
  28. ↑ Demaine, Erik D.; Schulz, André (2011), "Embedding stacked polytopes on a polynomial-size grid", Proc. 22nd ACM-SIAM Symp. Discrete Algorithms (SODA '11), pp. 1177–1187.
  29. ↑ Aichholzer, Oswin; Cheng, Howard; Devadoss, Satyan L.; Hackl, Thomas; Huber, Stefan; Li, Brian; Risteski, Andrej (2012), "What makes a Tree a Straight Skeleton?" (PDF), Proceedings of the 24th Canadian Conference on Computational Geometry (CCCG'12).
  30. ↑ Barnette, David W.; Grünbaum, Branko (1970), "Preassigning the shape of a face", Pacific J. Math., 32: 299–306, doi:10.2140/pjm.1970.32.299, MR 0259744.
  31. ↑ Barnette, David W. (1970), "Projections of 3-polytopes", Israel Journal of Mathematics, 8 (3): 304–308, doi:10.1007/BF02771563.
  32. ↑ Hart, George W. (1997), "Calculating canonical polyhedra", Mathematica in Education and Research, 6 (3): 5–10.
  33. ↑ Bern, Marshall; Eppstein, David (2001), "Optimal Möbius transformations for information visualization and meshing", Proc. 7th Worksh. Algorithms and Data Structures (WADS 2001), Lect. Notes Comp. Sci., 2125, Springer, pp. 14–25, doi:10.1007/3-540-44634-6_3.
  34. ↑ Schramm, Oded (1992), "How to cage an egg", Inventiones Mathematicae, 107 (3): 543–560, doi:10.1007/BF01231901, MR 1150601.
  35. ↑ Rivin, Igor (1996), "A characterization of ideal polyhedra in hyperbolic 3-space", Ann. of Math. (2nd Ser.), 143 (1): 51–70, doi:10.2307/2118652, MR 1370757.
  36. ↑ Dillencourt, Michael B.; Smith, Warren D. (1996), "Graph-theoretical conditions for inscribability and Delaunay realizability", Discrete Math., 161 (1-3): 63–77, doi:10.1016/0012-365X(95)00276-3, MR 1420521.
  37. ↑ Richter-Gebert, Jürgen (1996). Realization Spaces of Polytopes. Lecture Notes in Mathematics. 1643. Springer-Verlag. ISBN 978-3-540-62084-6.
  38. ↑ Hong, Seok-Hee; Nagamochi, Hiroshi (2011), "Extending Steinitz's theorem to upward star-shaped polyhedra and spherical polyhedra", Algorithmica, 61 (4): 1022–1076, doi:10.1007/s00453-011-9570-x, MR 2852056.
  39. ↑ Eppstein, David; Mumford, Elena (2014), "Steinitz theorems for simple orthogonal polyhedra", J. Comput. Geom., 5 (1): 179–244, MR 3259910.
  40. ↑ Blind, Roswitha; Mani-Levitska, Peter (1987), "Puzzles and polytope isomorphisms", Aequationes Mathematicae, 34 (2-3): 287–297, doi:10.1007/BF01830678, MR 921106.
  41. ↑ Kalai, Gil (1988), "A simple way to tell a simple polytope from its graph", Journal of Combinatorial Theory, Series A, 49 (2): 381–383, doi:10.1016/0097-3165(88)90064-7, MR 964396.
  42. ↑ Eppstein, David (2016), "Treetopes and their graphs", Proc. 27th ACM-SIAM Symp. Discrete Algorithms (SODA '16).
  43. ↑ Ziegler, Günter M. (2008), "Polyhedral surfaces of high genus", Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer, pp. 191–213, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7, MR 2405667.
  44. ↑ Lovász, László (2001), "Steinitz representations of polyhedra and the Colin de Verdière number", Journal of Combinatorial Theory, Series B, 82 (2): 223–236, doi:10.1006/jctb.2000.2027, MR 1842113.
This article is issued from Wikipedia - version of the 11/13/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.