Deficient number

Demonstration, with Cuisenaire rods, of the deficiency of the number 8

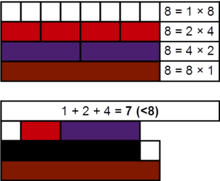
In number theory, a deficient or deficient number is a number n for which the sum of divisors σ(n)<2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)<n. The value 2n − σ(n) (or n − s(n)) is called the number's deficiency.

Examples

The first few deficient numbers are: :1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 46, 47, 49, 50, ... (sequence A005100 in the OEIS) As an example, consider the number 21. Its proper divisors are 1, 3 and 7, and their sum is 11. Because 11 is less than 21, the number 21 is deficient. Its deficiency is 2 × 21 − 32 = 10.

Properties

• Since the aliquot sums of prime numbers equal 1, all prime numbers are deficient.
• An infinite number of both even and odd deficient numbers exist.
• All odd numbers with one or two distinct prime factors are deficient.
• All proper divisors of deficient or perfect numbers are deficient.
• There exists at least one deficient number in the interval $[n, n + (\log n)^2]$ for all sufficiently large n.^[1]

Related concepts

Closely related to deficient numbers are perfect numbers with σ(n) = 2n, and abundant numbers with σ(n) > 2n. The natural numbers were first classified as either deficient, perfect or abundant by Nicomachus in his Introductio Arithmetica (circa 100).

See also

• Almost perfect number
• Amicable number
• Sociable number

References

1. Sándor et al (2006) p.108

• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. ISBN 1-4020-4215-9. Zbl 1151.11300.

External links

• The Prime Glossary: Deficient number
• Weisstein, Eric W. "Deficient Number". MathWorld.

• deficient number at PlanetMath.org.