Raised cosine distribution
|
Probability density function
| |
|
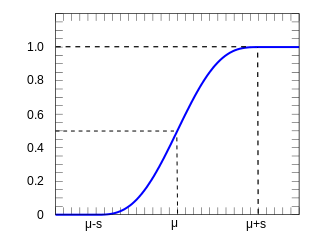
Cumulative distribution function
| |
| Parameters |
(real) |
|---|---|
| Support | |
| CDF | |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| MGF | |
| CF | |
In probability theory and statistics, the raised cosine distribution is a continuous probability distribution supported on the interval . The probability density function (PDF) is
for and zero otherwise. The cumulative distribution function (CDF) is
for and zero for and unity for .
The moments of the raised cosine distribution are somewhat complicated, but are considerably simplified for the standard raised cosine distribution. The standard raised cosine distribution is just the raised cosine distribution with and . Because the standard raised cosine distribution is an even function, the odd moments are zero. The even moments are given by:
where is a generalized hypergeometric function.
Differential equation
The pdf of the raised cosine distribution is a solution to the following differential equation:
See also
- Hann function
- Havercosine (hvc)
References
- Horst Rinne (2010). "Location-Scale Distributions - Linear Estimation and Probability Plotting Using MATLAB" (PDF). p. 116. Retrieved 2012-11-16.