Balding–Nichols model

Balding-Nichols
Probability density function
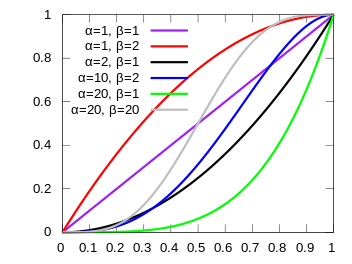
Cumulative distribution function
Parameters	$0<F<1$ (real) $0<p<1$ (real) For ease of notation, let $\alpha ={\tfrac {1-F}{F}}p$ , and $\beta ={\tfrac {1-F}{F}}(1-p)$
Support	$x\in (0;1)\!$
PDF	${\frac {x^{{\alpha -1}}(1-x)^{{\beta -1}}}{{\mathrm {B}}(\alpha ,\beta )}}\!$
CDF	$I_x(\alpha,\beta)\!$
Mean	$p\!$
Median	$I_{{0.5}}^{{-1}}(\alpha ,\beta )$ no closed form
Mode	${\frac {F-(1-F)p}{3F-1}}$
Variance	$Fp(1-p)\!$
Skewness	${\frac {2F(1-2p)}{(1+F){\sqrt {F(1-p)p}}}}$
MGF	$1+\sum _{{k=1}}^{{\infty }}\left(\prod _{{r=0}}^{{k-1}}{\frac {\alpha +r}{{\frac {1-F}{F}}+r}}\right){\frac {t^{k}}{k!}}$
CF	${}_1F_1(\alpha; \alpha+\beta; i\,t)\!$

In population genetics, the Balding–Nichols model is a statistical description of the allele frequencies in the components of a sub-divided population.^[1] With background allele frequency p the allele frequencies, in sub-populations separated by Wright's F_ST F, are distributed according to independent draws from

B\left({\frac {1-F}{F}}p,{\frac {1-F}{F}}(1-p)\right)

where B is the Beta distribution. This distribution has mean p and variance Fp(1 – p).^[2]

The model is due to David Balding and Richard Nichols and is widely used in the forensic analysis of DNA profiles and in population models for genetic epidemiology.

Differential equation

$\left\{F(x-1)xf'(x)+f(x)(F(-p)+3Fx-F+p-x)=0\right\}$

References

↑ Balding, DJ; Nichols, RA (1995). "A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity.". Genetica. Springer. 96: 3–12. doi:10.1007/BF01441146. PMID 7607457.
↑ Alkes L. Price; Nick J. Patterson; Robert M. Plenge; Michael E. Weinblatt; Nancy A. Shadick; David Reich (2006). "Principal components analysis corrects for stratification in genome-wide association studies" (PDF). Nature Genetics. 38 (8): 904–909. doi:10.1038/ng1847. PMID 16862161.

Population genetics

Key concepts	Hardy-Weinberg law Genetic linkage Identity by descent Linkage disequilibrium Fisher's fundamental theorem Neutral theory Shifting balance theory Price equation Coefficient of relationship Fitness Heritability

Selection	Natural Sexual Artificial Ecological

Effects of selection on genomic variation	Genetic hitchhiking Background selection

Genetic drift	Small population size Population bottleneck Founder effect Coalescence Balding–Nichols model

Founders	R. A. Fisher J. B. S. Haldane Sewall Wright

Related topics	Evolution Microevolution Evolutionary game theory Fitness landscape Genetic genealogy Quantitative genetics

List of evolutionary biology topics

Probability distributions

List

Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle

Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Flory–Schulz Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda

Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate	rectified Gaussian

Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular	Degenerate Dirac delta function Singular Cantor

Families	Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia - version of the 6/26/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.