30 (number)

← 29 30 31 →
← 30 31 32 33 34 35 36 37 38 39 → List of numbers — Integers ← 0 10 20 30 40 50 60 70 80 90 →
Cardinal	thirty
Ordinal	30th (thirtieth)
Numeral system	trigesimal
Factorization	2 × 3 × 5
Divisors	1, 2, 3, 5, 6, 10, 15, 30
Roman numeral	XXX
Binary	111102
Ternary	10103
Quaternary	1324
Quinary	1105
Senary	506
Octal	368
Duodecimal	2612
Hexadecimal	1E16
Vigesimal	1A20
Base 36	U36

30 (thirty) is the natural number following 29 and preceding 31.

In mathematics

30 is the sum of the first four squares, which makes it a square pyramidal number.^[1]

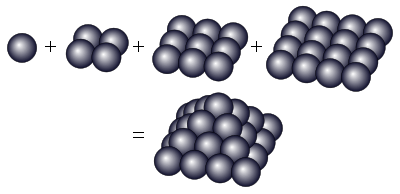
It is a primorial^[2] and is the smallest Giuga number.^[3]

30 is the smallest sphenic number, and the smallest of the form 2 × 3 × r, where r is a prime greater than 3. 30 has an aliquot sum of 42; the second sphenic number and all sphenic numbers of this form have an aliquot sum 12 greater than themselves. The aliquot sequence of 30 is 16 members long, it comprises (30,42,54,66,78,90,144,259,45,33,15,9,4,3,1,0)

Thirty has but one number for which it is the aliquot sum:^[4] the square number 841.^[5]

Adding up some subsets of its divisors (e.g., 5, 10 and 15) gives 30, hence 30 is a semiperfect number.^[6]

30 is the largest number such that all coprimes smaller than itself, except for 1, are prime.^[7]

A polygon with thirty sides is called a triacontagon.

The icosahedron and the dodecahedron are Platonic solids with 30 edges. The icosidodecahedron is an Archimedean solid with 30 vertices, and the Tutte–Coxeter graph is a symmetric graph with 30 vertices.

E₈ has Coxeter number 30.

30 is a Harshad number.^[8]

Since any group G such that |G| = pⁿm, where p does not divide m, has a subgroup of order pⁿ, and 30 is the only number less than 60 that is not either a prime or of the above form, it is the only candidate for the order of a simple group less than 60 that one needs other methods to reject.

In science

• The atomic number of zinc is 30

Astronomy

• Messier object M30, a magnitude 8.5 globular cluster in the constellation Capricornus
• The New General Catalogue object NGC 30, a double star in the constellation Pegasus
• The Saros number of the solar eclipse series which began on October 2, 2069 BC and ended on March 18, 572 BC. The duration of Saros series 30 was 1496.5 years, and it contained 84 solar eclipses. Further, the Saros number of the lunar eclipse series which began on June 19, 1803 BC and ended on August 18, 487 BC. The duration of Saros series 30 was 1316.2 years, and it contained 74 lunar eclipses.

In other fields

Thirty is:

• Used (as –30–) to indicate the end of a newspaper (or broadcast) story, a copy editor's typographical notation.
• The number of days in the months April, June, September and November (and in unusual circumstances February—see February 30)
• The total number of major and minor keys in Western tonal music, including enharmonic equivalents
• The minimum age for United States senators
• In years of marriage, the pearl wedding anniversary
• The duration in years of the Thirty Years' War - 1618 to 1648.
• The code for international direct dial phone calls to Greece
• The house number of 30 St Mary Axe (The Gherkin)
• The designation of Interstate 30, a freeway that runs from Texas to Arkansas
• The designation of U.S. Route 30, a highway that runs from Oregon to New Jersey
• Various other routes have been numbered "30"; for example, New York State Route 30 which runs from the NY–Pennsylvania border to the Canada–US border
• The designation of E30, the European route from Cork to Samara
• The number of tracks on The Beatles' eponymous album, usually known as The White Album
• A stage in young adulthood
• Part of the name of:
  • 30 Odd Foot of Grunts, the band fronted by actor Russell Crowe
  • The movie title 13 Going on 30, starring Jennifer Garner
  • The title of the Food Network show 30 Minute Meals
  • 30 Days of Night, a comic book miniseries and film.
• Judas Iscariot betrayed Jesus for 30 pieces of silver. Matthew 26:15.
• The number of the French department Gard
• 30 was the route number of the bus blown up by terrorists in Tavistock Square during the 7 July 2005 London bombings^[9]

History and literature

• At about age 30 (according to Luke 3:23), Jesus of Nazareth was baptized by John the Baptist, at the beginning of his public ministry of teaching and healing.
• One of the rallying-cries of the 1960s student/youth protest movement was the slogan, 'Don't trust anyone over thirty'.
• In 'The Myth of Sisyphus' the French existentialist Albert Camus comments that the age of thirty is a crucial period in the life of a man, for at that age he gains a new awareness of the meaning of time.
• In Franz Kafka's novel 'The Trial' Joseph wakes up on the morning of his thirtieth birthday to find himself under arrest for an unspecified crime. After making many futile attempts to find the nature of the crime or the name of his accuser, Joseph dies on the eve of his thirty-first birthday.
• The number of uprights that formed the Sarsen Circle at Stonehenge, also the supposed number of holes forming the arrays of Y and Z Holes at Stonehenge.
• Western Christianity's most prolific 20th century essayist, F. W. Boreham in 'Life at Thirty' ('Cliffs of Opal') mentions that in addition to Jesus commencing ministry at 30 (Luke 3:23), Joseph was 30 when he stood before Pharaoh, King of Egypt (Genesis 41:46), King David was 30 when he began to reign (2 Samuel 5:4), and the Levites were numbered from the age of 30 and upward (1 Chronicles 23:3). Also in that essay Boreham writes 'It was said of [the English poet] Keats, that "he ensphered himself in thirty perfect years and died, not young".'

Sports

• In tennis, the number 30 represents the second point gained in a game.
• Under NCAA rules for women's basketball, the offensive team has 30 seconds to attempt a shot.
• As of 2012, three of the four traditional major leagues in the United States and Canada (MLB, the NBA, and the NHL) have 30 teams each.
• The California Angels (now Los Angeles Angels of Anaheim) baseball team retired the number in honor of its most notable wearer, Nolan Ryan, on June 16, 1992. (Ryan is the only major league player to have his number retired by three different teams, though the other two teams retired number 34 for him rather than 30).^[10] The San Francisco Giants extended the same honor to Orlando Cepeda. While on the Chicago White Sox, Nick Swisher wore the number 30 and was known as "The Dirty 30".
• In basketball, Stephen Curry wears the number 30 jersey currently for the Golden State Warriors. He is the two time NBA MVP for 2015 and 2016. Along with his dad Dell Curry, he first wore the number 30 for the Cleveland Cavaliers, Milwaukee Bucks, Toronto Raptors, and the Utah Jazz.

Music

• The number of variations in Bach's Goldberg Variations
• 30, album from 2001 by Harry Connick, Jr.
• Thirty Seconds to Mars
• 30 Minutes, a song by t.A.T.u
• Thirty, 2013 album by Anthony Callea

References

1. "Sloane's A000330 : Square pyramidal numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
2. "Sloane's A002110 : Primorial numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
3. "Sloane's A007850 : Giuga numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
4. "Sloane's A057709 : Numbers n such that there is a unique x for which the sum of the aliquot parts of x". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation..
5. "Sloane's A070015 : Least m such that sum of aliquot parts of m equals n". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation..
6. "Sloane's A005835 : Pseudoperfect (or semiperfect) numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
7. Michael Slone, Every positive integer greater than 30 has at least one composite totative from PlanetMath. Accessed 24 April 2007
8. "Sloane's A005349 : Niven (or Harshad) numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
9. Report of the 7 July Review Committee Accessed 18 Dec 2011
10. Texas Rangers Retired Number History on mlb.com Retrieved May 18, 2006. Note however that Jackie Robinson's number 42 was retired by Major League Baseball for all teams.