Duopyramid
| Set of dual uniform p-q duopyramids | |
 Example 4-4 duopyramid (16-cell) Orthogonal projection | |
| Type | Uniform dual polychoron |
| Schläfli symbol | {p} + {q} |
| Coxeter diagram | |
| Cells | pq digonal disphenoids |
| Faces | 2pq triangles |
| Edges | pq+p+q |
| Vertices | p+q |
| Vertex figures | p-gonal bipyramid q-gonal bipyramid |
| Symmetry | [p,2,q], order 4pq |
| Dual | p-q duoprism |
| Properties | convex, facet-transitive |
| Set of dual uniform p-p duopyramids | |
| Schläfli symbol | {p} + {p} = 2{p} |
| Coxeter diagram | |
| Cells | p2 tetragonal disphenoids |
| Faces | 2p2 triangles |
| Edges | p2+2p |
| Vertices | 2p |
| Vertex figure | p-gonal bipyramid |
| Symmetry | p,2,p = [2p,2+,2p], order 8p2 |
| Dual | p-p duoprism |
| Properties | convex, facet-transitive |
In geometry of 4 dimensions or higher, a duopyramid is a dual polytope of a duoprism. As a dual uniform polychoron, it is called a p-q duopyramid with a composite Schläfli symbol {p} + {q}, and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The regular 16-cell can be seen as a 4-4 duopyramid, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , symmetry 4,2,4, order 128.
, symmetry 4,2,4, order 128.
A p-q duopyramid has Coxeter group symmetry [p,2,q], order 4pq. When p and q are identical, the symmetry is doubled as p,2,p, order 8p2.
Edges exist on all pairs of vertices between the p-gon and q-gon. The 1-skeleton of a p-q duopyramid represents edges of each p and q polygon and pq complete bipartite graph between them.
Geometry
A p-q duopyramid can be seen as two regular planar polygons of p and q sides with the same center and orthogonal orientations in 4 dimensions. Along with the p and q edges of the two polygons, all permutations of vertices in one polygon to vertices in the other form edges. All faces are triangular, with one edge of one polygon connected to one vertex of the other polygon. The p and q sided polygons are hollow, passing through the polytope center and not defining faces. Cells are tetrahedra constructed as all permutations of edge pairs between each polygon.
It can be understood by analogy to the relation of the 3D prisms and their dual bipyramids with Schläfli symbol { } + {p}, and a rhombus in 2D as { } + { }. A bipyramid can be seen as a 3D degenerated duopyramid, by adding an edge across the digon { } on the inner axis, and adding intersecting interior triangles and tetrahedra connecting that new edge to p-gon vertices and edges.
Other nonuniform polychora can be called duopyramids by the same construction, as two orthogonal and co-centered polygons, connected with edges with all combinations of vertex pairs between the polygons. The symmetry will be the product of the symmetry of the two polygons. So a rectangle-rectangle duopyramid would be topologically identical to the uniform 4-4 duopyramid, but a lower symmetry [2,2,2], order 16, possibly doubled to 32 if the two rectangles are identical.
Coordinates
The coordinates of a p-q duopyramid (on a unit 3-sphere) can be given as:
- (cos(2*πi/p),sin(2*πi/p),0,0), i=1..p
- (0,0,cos(2*πj/q),sin(2*πj/q)), j=1..q
All pairs of vertices are connected by edges.
Perspective projections
| 3-3 | 3-4 | 4-4 (16-cell) |
|---|---|---|
 |
 |
 |
Orthogonal projections
The 2n vertices of a n-n duopyramid can be orthogonally projected into two regular n-gons with edges between all vertices of each n-gon.
The regular 16-cell can be seen as a 4-4 duopyramid, being dual to the 4-4 duoprism, which is the tesseract. As a 4-4 duopyramid, the 16-cell's symmetry is [4,2,4], order 64, and doubled to 4,2,4, order 128 with the 2 central squares interchangeable. The regular 16-cell has a higher symmetry [3,3,4], order 384.
 3-3 |
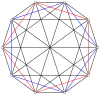 5-5 |
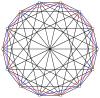 7-7 |
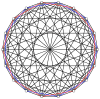 9-9 |
 11-11 |
 13-13 |
 15-15 |
 17-17 |
 19-19 |
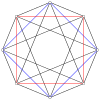 4-4 (16-cell) |
 6-6 |
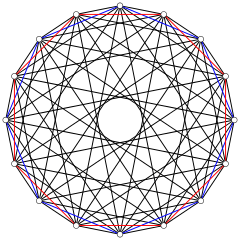 8-8 |
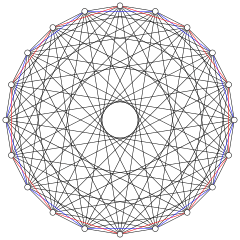 10-10 |
 12-12 |
 14-14 |
 16-16 |
 18-18 |
 20-20 |
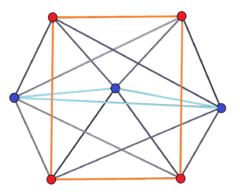 3-4 |
 3-5 |
 3-6 |
 3-8 |
 4-5 |
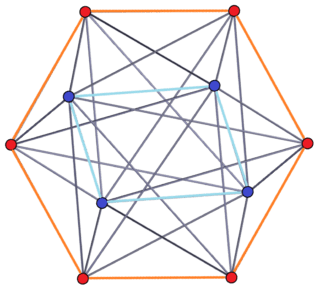 4-6 |
Example 6-4 duopyramid
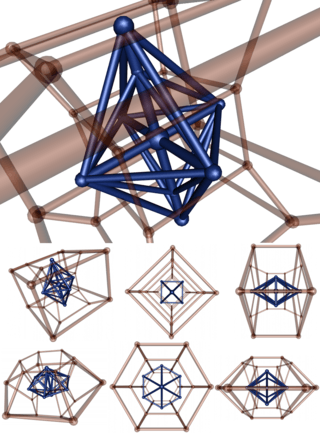 |
This vertex-centered stereographic projection of 6-4 duopyramid (blue) with its dual duoprism (in transparent red).
In the last row, the duopyramid is projected by a direction perpendicular to the first one; so the two parameters (6,4) seem to be reversed. Indeed, asymmetry is due to the projection: the two parameters are symmetric in 4D. |
References
- Olshevsky, George. "Duopyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polygloss - glossary of higher-dimensional terms