Multiview orthographic projection
| Part of a series on |
| Graphical projection |
|---|
 |

In technical drawing and computer graphics, a multiview orthographic projection is an illustration technique in which up to six pictures of an object are produced, with each projection plane parallel to one of the coordinate axes of the object.[1]
The views are positioned relative to each other according to either of two schemes: first-angle or third-angle projection. In each, the appearances of views may be thought of as being projected onto planes that form a 6-sided box around the object.
Primary views
Orthographic projections show the primary views of an object, each viewed in a direction parallel to one of the main coordinate axes. These primary views are called plans and elevations. Sometimes they are shown as if the object has been cut across or sectioned to expose the interior: these views are called sections.
Auxiliary views are sometimes taken from an angle that is not one of the primary views but these are not orthographic projections.[2][3]
Plan
A plan is a view of a 3-dimensional object seen from vertically above (or sometimes below). It may be drawn in the position of a horizontal plane passing through, above, or below the object. The outline of a shape in this view is sometimes called its planform, for example with aircraft wings.
The plan view from above a building is called its roof plan. A section seen in a horizontal plane through the walls and showing the floor beneath is called a floor plan.
Elevation

An elevation is a view of a 3-dimensional object from the position of a vertical plane beside an object. In other words, an elevation is a side-view as viewed from the front, back, left or right (and referred to as a front elevation, [left/ right] side elevation, and a rear elevation).
An elevation is a common method of depicting the external configuration and detailing of a 3-dimensional object in two dimensions. Building façades are shown as elevations in architectural drawings and technical drawings.
Elevations are the most common orthographic projection for conveying the appearance of a building from the exterior. Perspectives are also commonly used for this purpose. A building elevation is typically labeled in relation to the compass direction it faces; the direction from which a person views it. E.g. the North Elevation of a building is the side that most closely faces true north on the compass.[4]
Interior elevations are used to show detailing such as millwork and trim configurations.
In the building industry elevations are a non-perspective view of the structure. These are drawn to scale so that measurements can be taken for any aspect necessary. Drawing sets include front, rear and both side elevations. The elevations specify the composition of the different facades of the building, including ridge heights, the positioning of the final fall of the land, exterior finishes, roof pitches and other architectural details.
Developed Elevation
A developed elevation is a variant of a regular elevation view in which several adjacent non-parallel sides may be shown together, as if they have been unfolded. For example, the north and west views may be shown side-by-side, sharing an edge, even though this does not represent a proper orthographic projection.
Section
A section, or cross-section, is a view of a 3-dimensional object from the position of a plane through the object.
A section is a common method of depicting the internal arrangement of a 3-dimensional object in two dimensions. It is often used in technical drawing and is traditionally crosshatched. The style of crosshatching often indicates the type of material the section passes through.
With computed axial tomography, computers construct cross-sections from x-ray data.
-

A 3-D view of a beverage-can stove with a cross-section in yellow.
-
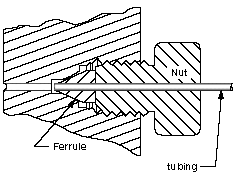
A 2-D cross-sectional view of a compression seal.
-

Half-section of a Porsche 996
Multi-view projections
First-angle projection
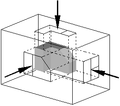
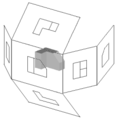
In first-angle projection, the object is conceptually located in quadrant I, i.e. it floats above and before the viewing planes, the planes are opaque, and each view is pushed through the object onto the plane furthest from it. (Mnemonic: an "actor on a stage".) Extending to the 6-sided box, each view of the object is projected in the direction (sense) of sight of the object, onto the (opaque) interior walls of the box; that is, each view of the object is drawn on the opposite side of the box. A two-dimensional representation of the object is then created by "unfolding" the box, to view all of the interior walls. This produces two plans and four elevations. A simpler way to visualize this is to place the object on top of an upside-down bowl. Sliding the object down the right edge of the bowl reveals the right side view.
-

Image of object in box, with views of object projected in the direction of sight onto walls using first-angle projection.
-
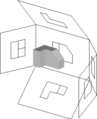
Similar image showing the box unfolding from around the object.
-

Image showing orthographic views located relative to each other in accordance with first-angle projection.
Third-angle projection
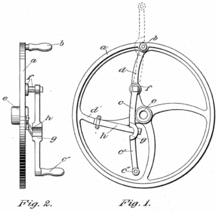
In third-angle projection, the object is conceptually located in quadrant III, i.e. it is positioned below and behind the viewing planes, the planes are transparent, and each view is pulled onto the plane closest to it. (Mnemonic: a "shark in a tank", esp. that is sunken into the floor.) Using the 6-sided viewing box, each view of the object is projected opposite to the direction (sense) of sight, onto the (transparent) exterior walls of the box; that is, each view of the object is drawn on the same side of the box. The box is then unfolded to view all of its exterior walls. A simpler way to visualize this is to place the object in the bottom of a bowl. Sliding the object up the right edge of the bowl reveals the right side view.
Here is the construction of third angle projections of the same object as above. Note that the individual views are the same, just arranged differently.
Additional information
First-angle projection is as if the object were sitting on the paper and, from the "face" (front) view, it is rolled to the right to show the left side or rolled up to show its bottom. It is standard throughout Europe and Asia (excluding Japan). First-angle projection was widely used in the UK, but during World War II, British drawings sent to be manufactured in the USA, such as of the Rolls-Royce Merlin, had to be drawn in third-angle projection before they could be produced, e.g., as the Packard V-1650 Merlin. This historical position of the UK means that some British companies completely adopted third angle projection. BS 308 (Part 1) Engineering Drawing Practice, gave the option of using both projections, but generally every illustration (other than the ones explaining the difference between first and third-angle) was done in first-angle. After the withdrawal of BS 308 in 1999, BS 8888 offered the same choice since it referred directly to ISO 5456-2, Technical drawings – Projection methods – Part 2: Orthographic representations.
Third-angle is as if the object were a box to be unfolded. If we unfold the box so that the front view is in the center of the two arms, then the top view is above it, the bottom view is below it, the left view is to the left, and the right view is to the right. It is standard in the USA (ASME Y14.3-2003 specifies it as the default projection system), Japan (JIS B 0001:2010 specifies it as the default projection system), Canada, and Australia.
Both first-angle and third-angle projections result in the same 6 views; the difference between them is the arrangement of these views around the box.
A great deal of confusion has ensued in drafting rooms and engineering departments when drawings are transferred from one convention to another. On engineering drawings, the projection angle is denoted by an international symbol consisting of a truncated cone, respectively for first-angle and third-angle:
http://www3.ul.ie/~rynnet/orthographic_projection_fyp/images/projection_symbols.png
The 3D interpretation of the symbol can be deduced by envisioning a solid truncated cone, standing upright with its large end on the floor and the small end upward. The top view is therefore two concentric circles ("donut"). In particular, the fact that the inner circle is drawn with a solid line instead of dashed identifies this view as the top view, not the bottom view.
- In first-angle projection, the "top" view is pushed down to the floor, and the "front" view is pushed back to the rear wall; the intersection line between these two planes is therefore closest to the large end of the cone, hence the first-angle symbol shows the cone with its large end open toward the donut.
- In third-angle projection, the "top" view is pulled up to the ceiling, and the "front" view is pulled forward to the front wall; the intersection line between the two planes is thus closest to the small end of the cone, hence the third-angle symbol shows the cone with its large end away from the donut.
Multiviews without rotation
Orthographic multiview projection is derived from the principles of descriptive geometry and may produce an image of a specified, imaginary object as viewed from any direction of space. Orthographic projection is distinguished by parallel projectors emanating from all points of the imaged object and which intersect of projection at right angles. Above, a technique is described that obtains varying views by projecting images after the object is rotated to a desired position.
Descriptive geometry customarily relies on obtaining various views by imagining an object to be stationary, and changing the direction of projection (viewing) in order to obtain the desired view.
See Figure 1. Using the rotation technique above, note that no orthographic view is available looking perpendicularly at any of the inclined surfaces. Suppose a technician desired such a view to, say, look through a hole to be drilled perpendicularly to the surface. Such a view might be desired for calculating clearances or for dimensioning purposes. To obtain this view without multiple rotations requires the principles of Descriptive Geometry. The steps below describe the use of these principles in third angle projection.
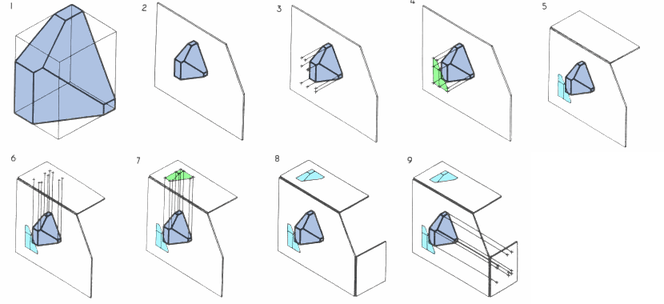
- Fig.1: Pictorial of imaginary object that the technician wishes to image.
- Fig.2: The object is imagined behind a vertical plane of projection. The angled corner of the plane of projection is addressed later.
- Fig.3: Projectors emanate parallel from all points of the object, perpendicular to the plane of projection.
- Fig.4: An image is created thereby.
- Fig.5: A second, horizontal plane of projection is added, perpendicular to the first.
- Fig.6: Projectors emanate parallel from all points of the object perpendicular to the second plane of projection.
- Fig.7: An image is created thereby.
- Fig.8: A third plane of projection is added, perpendicular to the previous two.
- Fig.9: Projectors emanate parallel from all points of the object perpendicular to the third plane of projection.
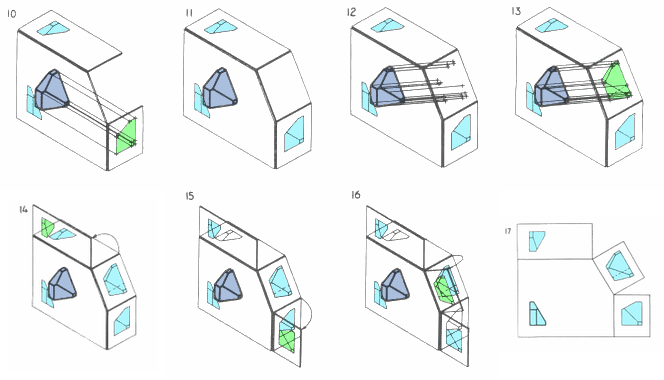
- Fig.10: An image is created thereby.
- Fig.11: A fourth plane of projection is added parallel to the chosen inclined surface, and per force, perpendicular to the first (Frontal) plane of projection.
- Fig.12: Projectors emanate parallel from all points of the object perpendicularly from the inclined surface, and per force, perpendicular to the fourth (Auxiliary) plane of projection.
- Fig.13: An image is created thereby.
- Fig.14-16: The various planes of projection are unfolded to be planar with the Frontal plane of projection.
- Fig.17: The final appearance of an orthographic multiview projection and which includes an "Auxiliary view" showing the true shape of an inclined surface.
Territorial use
Europe and Most of the World
First Angle is used in most of the world.[5]
America
Third angle projection is most commonly used in America[6]
Australia
Third Angle Projection is preferred in Australia, as laid down in AS 1100.101—1992 6.3.3[7]
Great Britain
BS8888 9.7.2.1 allows for three different conventions for arranging views, these are: Labelled Views, Third Angle Projection, and First Angle Projection.
See also
- Architectural drawing
- Cross section (geometry)
- Engineering drawing
- Graphical projection
- Plans (drawings)
References
- ↑ Ingrid Carlbom, Joseph Paciorek (1978), "Planar Geometric Projections and Viewing Transformations", ACM Computing Surveys, 10 (4): 465–502, doi:10.1145/356744.356750
- ↑ Illustrator Draftsman 3 & 2 - Volume 2 Standard Practices and Theory, pages 3/49-3/50, from tpub.com
- ↑ Dorn, Dennis; Shanda, Mark (1992), Drafting for the theatre, SIU Press, p. 90, ISBN 0-8093-1508-4
- ↑ Ching, Frank (1985), Architectural Graphics - Second Edition, New York: Van Norstrand Reinhold, ISBN 0-442-21862-1
- ↑ http://www3.ul.ie/~rynnet/orthographic_projection_fyp/webpages/third_angle.html
- ↑ https://books.google.com/books?id=spdxCwAAQBAJ&pg=PA234&lpg=PA234&dq=asme+y14.3&source=bl&ots=Y-LDefoeGq&sig=6eEmEixLZMufehl3MD2gSdoGVes&hl=en&sa=X&ved=0ahUKEwjyls65nPPKAhVDuRQKHSCzCP84FBDoAQgeMAA#v=onepage&q=asme%20y14.3&f=false
- ↑ https://archive.org/stream/AS1100.1011992TechnicalDwgs/AS1100.101-1992%20Technical%20Dwgs_djvu.txt
BS 308 (Part 1) Engineering Drawing Practice BS 8888 Technical product documentation and specification ISO 5456-2 Technical drawings – Projection methods – Part 2: Orthographic Representations (includes the truncated cone symbol)
External links
- Educational website describing the principles of first and third angle projection — University of Limerick
- Educational website describing the principles of first and third angle projection
- Images tagged "Elevation" on Flickr.com
- Basic Projection Method first angle vs third angle