Pentakis dodecahedron

Pentakis dodecahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	kD
Face type	V5.6.6 isosceles triangle
Faces	60
Edges	90
Vertices	32
Vertices by type	20{6}+12{5}
Symmetry group	Ih, H3, [5,3], (*532)
Rotation group	I, [5,3]^+, (532)
Dihedral angle	156°43′07″ arccos(−80 + 9√5/109)
Properties	convex, face-transitive
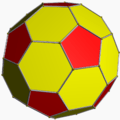Truncated icosahedron (dual polyhedron)	Net

In geometry, a pentakis dodecahedron or kisdodecahedron is a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron. This interpretation is expressed in its name.^[1] There are in fact several topologically equivalent but geometrically distinct kinds of pentakis dodecahedron, depending on the height of the pentagonal pyramids. These include:

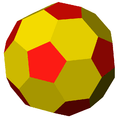
• The usual Catalan pentakis dodecahedron, a convex hexecontahedron with sixty isosceles triangular faces illustrated in the sidebar figure. It is a Catalan solid, dual to the truncated icosahedron, an Archimedean solid.
• As the heights of the pentagonal pyramids are raised, at a certain point adjoining pairs of triangular faces merge to become rhombi, and the shape becomes a rhombic triacontahedron.
• As the height is raised further, the shape becomes non-convex. In particular, an equilateral or deltahedron version of the pentakis dodecahedron, which has sixty equilateral triangular faces as shown in the adjoining figure, is slightly non-convex due to its taller pyramids (note, for example, the negative dihedral angle at the upper left of the figure).

Other more non-convex geometric variants include:

• The small stellated dodecahedron (with very tall pyramids).
• Great pentakis dodecahedron (with extremely tall pyramids)
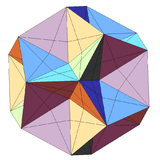• Wenninger's third stellation of icosahedron (with inverted pyramids).

If one affixes pentagrammic pyramids into Wenninger's third stellation of icosahedron one obtains the great icosahedron.

Chemistry

The pentakis dodecahedron in a model of buckminsterfullerene: each surface segment represents a carbon atom. Equivalently, a truncated icosahedron is a model of buckminsterfullerene, with each vertex representing a carbon atom.

Biology

The pentakis dodecahedron is also a model of some icosahedrally symmetric viruses, such as Adeno-associated virus. These have 60 symmetry related capsid proteins, which combine to make the 60 symmetrical faces of a pentakis dodecahedron.

Orthogonal projections

The pentakis dodecahedron has three symmetry positions, two on vertices, and one on a midedge:

Orthogonal projections

Projective symmetry	[2]	[6]	[10]
Image
Dual image

Related polyhedra

Spherical pentakis dodecahedron

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)							[5,3]^+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

*n32 symmetry mutation of truncated tilings: n.6.6
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Cultural references

• The Spaceship Earth structure at Walt Disney World's Epcot is a derivative of a pentakis dodecahedron.
• The model for a campus arts workshop designed by Jeffrey Lindsay was actually a hemispherical pentakis dodecahedron https://books.google.com/books?id=JD8EAAAAMBAJ&pg=PA92&dq=jeffrey+lindsay&hl=en&ei=oF88Tv25F7OisQLGwbwt&sa=X&oi=book_result&ct=result&redir_esc=y#v=onepage&q=jeffrey%20lindsay&f=false
• The shape of the "Crystal Dome" used in the popular TV game show The Crystal Maze was based on a pentakis dodecahedron.
• In Doctor Atomic, the shape of the first atomic bomb detonated in New Mexico was a pentakis dodecahedron.
• In De Blob 2 in the Prison Zoo, domes are made up of parts of a Pentakis Dodecahedron. These Domes also appear whenever the player transforms on a dome in the Hypno Ray level.
• Some Geodomes in which people play on are Pentakis Dodecahedra.

References

1. Conway, Symmetries of things, p.284

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Sellars, Peter (2005). "Doctor Atomic Libretto". Boosey & Hawkes. We surround the plutonium core from thirty two points spaced equally around its surface, the thirty-two points are the centers of the twenty triangular faces of an icosahedron interwoven with the twelve pentagonal faces of a dodecahedron.
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 730208. (The thirteen semiregular convex polyhedra and their duals, Page 18, Pentakisdodecahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Pentakis dodecahedron )

External links

• Eric W. Weisstein, Pentakis dodecahedron (Catalan solid) at MathWorld.
• Pentakis Dodecahedron – Interactive Polyhedron Model