Stellated octahedron
| Stellated octahedron | |
|---|---|
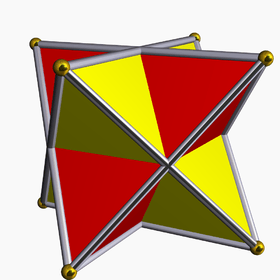 Seen as a compound of two regular tetrahedra (red and yellow) | |
| Type | Regular compound |
| Coxeter symbol | {4,3}[2{3,3}]{3,4}[1] |
| Schläfli symbols | {{3,3}} a{4,3} ß{2,4} ßr{2,2} |
| Coxeter diagrams | |
| Stellation core | Octahedron |
| Convex hull | Cube |
| Index | UC4, W19 |
| Polyhedra | 2 tetrahedra |
| Faces | 8 triangles |
| Edges | 12 |
| Vertices | 8 |
| Dual | Self-dual |
| Symmetry group Coxeter group | Oh, [4,3], order 48 D4h, [4,2], order 16 D2h, [2,2], order 8 D3d, [2+,6], order 12 |
| Subgroup restricting to one constituent | Td, [3,3], order 24 D2d, [2+,4], order 8 D2, [2,2]+, order 4 C3v, [3], order 6 |
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's Divina Proportione, 1509.[2]
It is the simplest of five regular polyhedral compounds, and the only regular compound of two tetrahedra.
It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. It can also be seen as one of the stages in the construction of a 3D Koch Snowflake, a fractal shape formed by repeated attachment of smaller tetrahedra to each triangular face of a larger figure. The first stage of the construction of the Koch Snowflake is a single central tetrahedron, and the second stage, formed by adding four smaller tetrahedra to the faces of the central tetrahedron, is the stellated octahedron.
Construction
The stellated octahedron can be constructed in several ways:
- It is a stellation of the regular octahedron, sharing the same face planes. (See Wenninger model W19.)
 In perspective |  Stellation plane | The only stellation of a regular octahedron, with one stellation plane in yellow. |
- It is also a regular polyhedron compound, when constructed as the union of two regular tetrahedra (a regular tetrahedron and its dual tetrahedron).
- It can be obtained as an augmentation of the regular octahedron, by adding tetrahedral pyramids on each face. In this construction it has the same topology as the convex Catalan solid, the triakis octahedron, which has much shorter pyramids.
- It is a facetting of the cube, sharing the vertex arrangement.
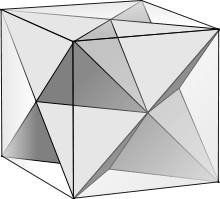 Facetting of a cube |
 A single diagonal triangle facetting in red |
Related concepts
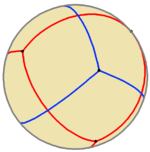
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, between two parallel edges of the two tetrahedra. These two tetrahedra can be completed to a desmic system of three tetrahedra, where the third tetrahedron has as its four vertices the three crossing points at infinity and the centroid of the two finite tetrahedra. The same twelve tetrahedron vertices also form the points of Reye's configuration.
The stella octangula numbers are figurate numbers that count the number of balls that can be arranged into the shape of a stellated octahedron. They are
In popular culture
The stellated octahedron appears with several other polyhedra and polyhedral compounds in M. C. Escher's print "Stars",[3] and provides the central form in Escher's Double Planetoid (1949).[4]
Gallery
 |
 |
 |
 |
 |
 |
References
- ↑ Regular polytopes, pp.48-50, p.98
- ↑ Barnes, John (2009), "Shapes and Solids", Gems of Geometry, Springer, pp. 25–56, doi:10.1007/978-3-642-05092-3_2, ISBN 978-3-642-05091-6.
- ↑ Hart, George W. (1996), "The Polyhedra of M.C. Escher", Virtual Polyhedra.
- ↑ Coxeter, H. S. M. (1985), "A special book review: M. C. Escher: His life and complete graphic work", The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010. See in particular p. 61.
- Peter R. Cromwell, Polyhedra, Cambridge University Press (1997) Polyhedra
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
External links
| Wikimedia Commons has media related to Stellated octahedron. |
- Klitzing, Richard. "3D compound".