5-polytope
 5-simplex (hexateron) |
 5-orthoplex, 211 (Pentacross) |
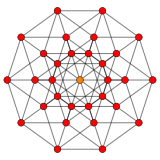 5-cube (Penteract) |
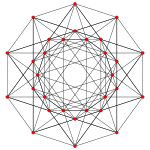 Expanded 5-simplex |
 Rectified 5-orthoplex |
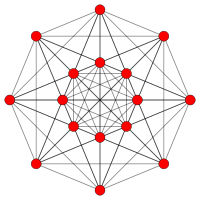 5-demicube. 121 (Demipenteract) |
In five-dimensional geometry, a five-dimensional polytope or 5-polytope is a 5-dimensional polytope, bounded by (4-polytope) facets. Each polyhedral cell being shared by exactly two 4-polytope facets.
Definition
A 5-polytope is a closed five-dimensional figure with vertices, edges, faces, and cells, and 4-faces. A vertex is a point where five or more edges meet. An edge is a line segment where four or more faces meet, and a face is a polygon where three or more cells meet. A cell is a polyhedron, and a 4-face is a 4-polytope. Furthermore, the following requirements must be met:
- Each cell must join exactly two 4-faces.
- Adjacent 4-faces are not in the same four-dimensional hyperplane.
- The figure is not a compound of other figures which meet the requirements.
Characteristics
The topology of any given 5-polytope is defined by its Betti numbers and torsion coefficients.[1]
The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.[1]
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.[1]
Classification
5-polytopes may be classified based on properties like "convexity" and "symmetry".
- A 5-polytope is convex if its boundary (including its cells, faces and edges) does not intersect itself and the line segment joining any two points of the 5-polytope is contained in the 5-polytope or its interior; otherwise, it is non-convex. Self-intersecting 5-polytopes are also known as star polytopes, from analogy with the star-like shapes of the non-convex Kepler-Poinsot polyhedra.
- A uniform 5-polytope has a symmetry group under which all vertices are equivalent, and its facets are uniform 4-polytopes. The faces of a uniform polytope must be regular.
- A semi-regular 5-polytope contains two or more types of regular 4-polytope facets. There is only one such figure, called a demipenteract.
- A regular 5-polytope has all identical regular 4-polytope facets. All regular 5-polytopes are convex.
- A prismatic 5-polytope is constructed by a Cartesian product of two lower-dimensional polytopes. A prismatic 5-polytope is uniform if its factors are uniform. The hypercube is prismatic (product of a square and a cube), but is considered separately because it has symmetries other than those inherited from its factors.
- A 4-space tessellation is the division of four-dimensional Euclidean space into a regular grid of polychoral facets. Strictly speaking, tessellations are not polytopes as they do not bound a "5D" volume, but we include them here for the sake of completeness because they are similar in many ways to polytopes. A uniform 4-space tessellation is one whose vertices are related by a space group and whose facets are uniform 4-polytopes.
Regular 5-polytopes
Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} polychoral facets around each face.
There are exactly three such convex regular 5-polytopes:
- {3,3,3,3} - 5-simplex
- {4,3,3,3} - 5-cube
- {3,3,3,4} - 5-orthoplex
For the 3 convex regular 5-polytopes and three semiregular 5-polytope, their elements are:
| Name | Schläfli symbol(s) | Coxeter diagram(s) | Vertices | Edges | Faces | Cells | 4-faces | Symmetry (order) |
|---|---|---|---|---|---|---|---|---|
| 5-simplex | {3,3,3,3} | 6 | 15 | 20 | 15 | 6 | A5, (120) | |
| 5-cube | {4,3,3,3} | 32 | 80 | 80 | 40 | 10 | BC5, (3820) | |
| 5-orthoplex | {3,3,3,4} {3,3,31,1} | 10 | 40 | 80 | 80 | 32 | BC5, (3840) 2×D5 |
Uniform 5-polytopes
For three of the semiregular 5-polytope, their elements are:
| Name | Schläfli symbol(s) | Coxeter diagram(s) | Vertices | Edges | Faces | Cells | 4-faces | Symmetry (order) |
|---|---|---|---|---|---|---|---|---|
| Expanded 5-simplex | t0,4{3,3,3,3} | 30 | 120 | 210 | 180 | 162 | 2×A5, (240) | |
| 5-demicube | {3,32,1} h{4,3,3,3} | 16 | 80 | 160 | 120 | 26 | D5, (1920) ½BC5 | |
| Rectified 5-orthoplex | t1{3,3,3,4} t1{3,3,31,1} | 40 | 240 | 400 | 240 | 42 | BC5, (3840) 2×D5 |
The expanded 5-simplex is the vertex figure of the uniform 5-simplex honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . The 5-demicube honeycomb,
. The 5-demicube honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , vertex figure is a rectified 5-orthoplex and facets are the 5-orthoplex and 5-demicube.
, vertex figure is a rectified 5-orthoplex and facets are the 5-orthoplex and 5-demicube.
Pyramids
Pyramidal 5-polytopes, or 5-pyramids, can be generated by a 4-polytope base in a 4-space hyperplane connected to a point off the hyperplane. The 5-simplex is the simplest example with a 4-simplex base.
See also
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "5D uniform polytopes (polytera)".
External links
- Polytopes of Various Dimensions, Jonathan Bowers
- Uniform Polytera, Jonathan Bowers
- Olshevsky, George. "Polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Multi-dimensional Glossary, Garrett Jones
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||