Hypercubic honeycomb
 A regular square tiling. 1 color |
 A cubic honeycomb in its regular form. 1 color |
 A checkboard square tiling 2 colors |
 A cubic honeycomb checkerboard. 2 colors |
 Expanded square tiling 3 colors |
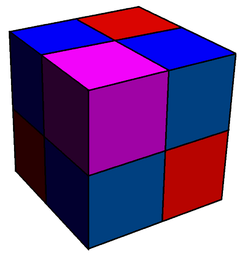 Expanded cubic honeycomb 4 colors |
 4 colors |
 8 colors |
In geometry, a hypercubic honeycomb is a family of regular honeycombs (tessellations) in n-dimensions with the Schläfli symbols {4,3...3,4} and containing the symmetry of Coxeter group Rn (or B~n-1) for n>=3.
The tessellation is constructed from 4 n-hypercubes per ridge. The vertex figure is a cross-polytope {3...3,4}.
The hypercubic honeycombs are self-dual.
Coxeter named this family as δn+1 for an n-dimensional honeycomb.
Wythoff construction classes by dimension
There are two general forms of the hypercube honeycombs, the regular form with identical hypercubic facets and one semiregular, with alternating hypercube facets, like a checkerboard.
A third form is generated by an expansion operation applied to the regular form, creating facets in place of all lower-dimensional elements. For example, an expanded cubic honeycomb has cubic cells centered on the original cubes, on the original faces, on the original edges, on the original vertices, creating 4 colors of cells around in vertex in 1:3:3:1 counts.
The orthotopic honeycombs are a family topologically equivalent to the cubic honeycombs but with lower symmetry, in which each of the three axial directions may have different edge lengths. The facets are hyperrectangles, also called orthotopes; in 2 and 3 dimensions the orthotopes are rectangles and cuboids respectively.
| δn | Name | Schläfli symbols | Coxeter-Dynkin diagrams | |||
|---|---|---|---|---|---|---|
| Orthotopic {∞}n (2m colors, m<n) |
Regular (Expanded) {4,3n-1,4} (1 color, n colors) |
Checkerboard {4,3n-4,31,1} (2 colors) | ||||
| δ2 | Apeirogon | {∞} | ||||
| δ3 | Square tiling | {∞}2 {4,4} |
||||
| δ4 | Cubic honeycomb | {∞}3 {4,3,4} {4,31,1} |
||||
| δ5 | 4-cube honeycomb | {∞}4 {4,32,4} {4,3,31,1} |
||||
| δ6 | 5-cube honeycomb | {∞}5 {4,33,4} {4,32,31,1} |
||||
| δ7 | 6-cube honeycomb | {∞}6 {4,34,4} {4,33,31,1} |
||||
| δ8 | 7-cube honeycomb | {∞}7 {4,35,4} {4,34,31,1} |
||||
| δ9 | 8-cube honeycomb | {∞}8 {4,36,4} {4,35,31,1} |
||||
| δn | n-hypercubic honeycomb | {∞}n {4,3n-3,4} {4,3n-4,31,1} |
... | |||
See also
- Alternated hypercubic honeycomb
- Quarter hypercubic honeycomb
- Simplectic honeycomb
- Truncated simplectic honeycomb
- Omnitruncated simplectic honeycomb
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 122–123, 1973. (The lattice of hypercubes γn form the cubic honeycombs, δn+1)
- pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- p. 296, Table II: Regular honeycombs, δn+1
| Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9) | |||||
|---|---|---|---|---|---|
| Family | / / | ||||
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform 10-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |