Uniform k 21 polytope
In geometry, a uniform k21 polytope is a polytope in k + 4 dimensions constructed from the En Coxeter group, and having only regular polytope facets. The family was named by their Coxeter symbol k21 by its bifurcating Coxeter–Dynkin diagram, with a single ring on the end of the k-node sequence.
Thorold Gosset discovered this family as a part of his 1900 enumeration of the regular and semiregular polytopes, and so they are sometimes called Gosset's semiregular figures. Gosset named them by their dimension from 5 to 9, for example the 5-ic semiregular figure.
Family members
The sequence as identified by Gosset ends as an infinite tessellation (space-filling honeycomb) in 8-space, called the E8 lattice. (A final form was not discovered by Gosset and is called the E9 lattice: 621. It is a tessellation of hyperbolic 9-space constructed of (∞ 9-simplex and ∞ 9-orthoplex facets with all vertices at infinity.)
The family starts uniquely as 6-polytopes. The triangular prism and rectified 5-cell are included at the beginning for completeness. The demipenteract also exists in the demihypercube family.
They are also sometimes named by their symmetry group, like E6 polytope, although there are many uniform polytopes within the E6 symmetry.
The complete family of Gosset semiregular polytopes are:
- triangular prism: −121 (2 triangles and 3 square faces)
- rectified 5-cell: 021, Tetroctahedric (5 tetrahedra and 5 octahedra cells)
- demipenteract: 121, 5-ic semiregular figure (16 5-cell and 10 16-cell facets)
- 2 21 polytope: 221, 6-ic semiregular figure (72 5-simplex and 27 5-orthoplex facets)
- 3 21 polytope: 321, 7-ic semiregular figure (567 6-simplex and 126 6-orthoplex facets)
- 4 21 polytope: 421, 8-ic semiregular figure (17280 7-simplex and 2160 7-orthoplex facets)
- 5 21 honeycomb: 521, 9-ic semiregular check tessellates Euclidean 8-space (∞ 8-simplex and ∞ 8-orthoplex facets)
- 6 21 honeycomb: 621, tessellates hyperbolic 9-space (∞ 9-simplex and ∞ 9-orthoplex facets)
Each polytope is constructed from (n − 1)-simplex and (n − 1)-orthoplex facets.
The orthoplex faces are constructed from the Coxeter group Dn−1 and have a Schläfli symbol of {31,n−1,1} rather than the regular {3n−2,4}. This construction is an implication of two "facet types". Half the facets around each orthoplex ridge are attached to another orthoplex, and the others are attached to a simplex. In contrast, every simplex ridge is attached to an orthoplex.
Each has a vertex figure as the previous form. For example, the rectified 5-cell has a vertex figure as a triangular prism.
Elements
| n-ic | k21 | Graph | Name Coxeter diagram |
Facets | Elements | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (n − 1)-simplex {3n−2} |
(n − 1)-orthoplex {3n−4,1,1} |
Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | ||||
| 3-ic | −121 | |
Triangular prism |
2 triangles |
3 squares |
6 | 9 | 5 | |||||
| 4-ic | 021 |  |
Rectified 5-cell |
5 tetrahedron |
5 octahedron |
10 | 30 | 30 | 10 | ||||
| 5-ic | 121 | 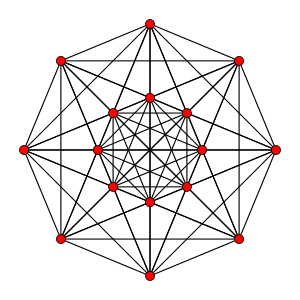 |
Demipenteract |
16 5-cell |
10 16-cell |
16 | 80 | 160 | 120 | 26 | |||
| 6-ic | 221 |  |
221 polytope |
72 5-simplexes |
27 5-orthoplexes |
27 | 216 | 720 | 1080 | 648 | 99 | ||
| 7-ic | 321 | 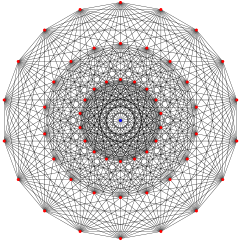 |
321 polytope |
576 6-simplexes |
126 6-orthoplexes |
56 | 756 | 4032 | 10080 | 12096 | 6048 | 702 | |
| 8-ic | 421 | 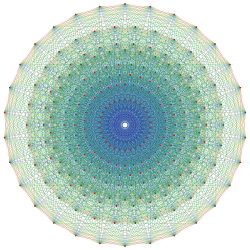 |
421 polytope |
17280 7-simplexes |
2160 7-orthoplexes |
240 | 6720 | 60480 | 241920 | 483840 | 483840 | 207360 | 19440 |
| 9-ic | 521 | 521 honeycomb |
∞ 8-simplexes |
∞ 8-orthoplexes |
∞ | ||||||||
| 10-ic | 621 | 621 honeycomb |
∞ 9-simplexes |
∞ 9-orthoplexes |
∞ | ||||||||
See also
- Uniform 2k1 polytope family
- Uniform 1k2 polytope family
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Alicia Boole Stott Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- Stott, A. B. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam 11, 3–24, 1910.
- Alicia Boole Stott, "Geometrical deduction of semiregular from regular polytopes and space fillings," Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, (eerste sectie), Vol. 11, No. 1, pp. 1–24 plus 3 plates, 1910.
- Stott, A. B. 1910. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam
- Schoute, P. H., Analytical treatment of the polytopes regularly derived from the regular polytopes, Ver. der Koninklijke Akad. van Wetenschappen te Amsterdam (eerstie sectie), vol 11.5, 1913.
- H. S. M. Coxeter: Regular and Semi-Regular Polytopes, Part I, Mathematische Zeitschrift, Springer, Berlin, 1940
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part II, Mathematische Zeitschrift, Springer, Berlin, 1985
- H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part III, Mathematische Zeitschrift, Springer, Berlin, 1988
- G.Blind and R.Blind, "The semi-regular polyhedra", Commentari Mathematici Helvetici 66 (1991) 150–154
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 411–413: The Gosset Series: n21)
External links
- PolyGloss v0.05: Gosset figures (Gossetoicosatope)
- Regular, SemiRegular, Regular faced and Archimedean polytopes
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
| Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9) | |||||
|---|---|---|---|---|---|
| Family | / / | ||||
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform 10-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |