Uniform 9-polytope

Graphs of three regular and related uniform polytopes

9-simplex						Rectified 9-simplex
Truncated 9-simplex						Cantellated 9-simplex
Runcinated 9-simplex						Stericated 9-simplex
Pentellated 9-simplex						Hexicated 9-simplex
Heptellated 9-simplex						Octellated 9-simplex
9-orthoplex						9-cube
Truncated 9-orthoplex						Truncated 9-cube
Rectified 9-orthoplex						Rectified 9-cube
9-demicube						Truncated 9-demicube

In nine-dimensional geometry, a nine-dimensional polytope or 9-polytope is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets.

A uniform 9-polytope is one which is vertex-transitive, and constructed from uniform 8-polytope facets.

Regular 9-polytopes

Regular 9-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v,w}, with w {p,q,r,s,t,u,v} 8-polytope facets around each peak.

There are exactly three such convex regular 9-polytopes:

{3,3,3,3,3,3,3,3} - 9-simplex
{4,3,3,3,3,3,3,3} - 9-cube
{3,3,3,3,3,3,3,4} - 9-orthoplex

There are no nonconvex regular 9-polytopes.

Euler characteristic

The topology of any given 9-polytope is defined by its Betti numbers and torsion coefficients.^[1]

The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.^[1]

Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.^[1]

Uniform 9-polytopes by fundamental Coxeter groups

Uniform 9-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:

Coxeter group		Coxeter-Dynkin diagram
A₉	[3⁸]
B₉	[4,3⁷]
D₉	[3^6,1,1]

Selected regular and uniform 9-polytopes from each family include:

Simplex family: A₉ [3⁸] -
- 271 uniform 9-polytopes as permutations of rings in the group diagram, including one regular:
  1. {3⁸} - 9-simplex or deca-9-tope or decayotton -
Hypercube/orthoplex family: B₉ [4,3⁸] -
- 511 uniform 9-polytopes as permutations of rings in the group diagram, including two regular ones:
  1. {4,3⁷} - 9-cube or enneract -
  2. {3⁷,4} - 9-orthoplex or enneacross -
Demihypercube D₉ family: [3^6,1,1] -
- 383 uniform 9-polytope as permutations of rings in the group diagram, including:
  1. {3^1,6,1} - 9-demicube or demienneract, 1₆₁ - ; also as h{4,3⁸} .
  2. {3^6,1,1} - 9-orthoplex, 6₁₁ -

The A₉ family

The A₉ family has symmetry of order 3628800 (10 factorial).

There are 256+16-1=271 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. These are all enumerated below. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	Element counts
#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	8-faces	7-faces	6-faces	5-faces	4-faces	Cells	Faces	Edges	Vertices
1		t₀{3,3,3,3,3,3,3,3} 9-simplex (day)	10	45	120	210	252	210	120	45	10
2		t₁{3,3,3,3,3,3,3,3} Rectified 9-simplex (reday)								360	45
3		t₂{3,3,3,3,3,3,3,3} Birectified 9-simplex (breday)								1260	120
4		t₃{3,3,3,3,3,3,3,3} Trirectified 9-simplex (treday)								2520	210
5		t₄{3,3,3,3,3,3,3,3} Quadrirectified 9-simplex (icoy)								3150	252
6		t_0,1{3,3,3,3,3,3,3,3} Truncated 9-simplex (teday)								405	90
7		t_0,2{3,3,3,3,3,3,3,3} Cantellated 9-simplex								2880	360
8		t_1,2{3,3,3,3,3,3,3,3} Bitruncated 9-simplex								1620	360
9		t_0,3{3,3,3,3,3,3,3,3} Runcinated 9-simplex								8820	840
10		t_1,3{3,3,3,3,3,3,3,3} Bicantellated 9-simplex								10080	1260
11		t_2,3{3,3,3,3,3,3,3,3} Tritruncated 9-simplex (treday)								3780	840
12		t_0,4{3,3,3,3,3,3,3,3} Stericated 9-simplex								15120	1260
13		t_1,4{3,3,3,3,3,3,3,3} Biruncinated 9-simplex								26460	2520
14		t_2,4{3,3,3,3,3,3,3,3} Tricantellated 9-simplex								20160	2520
15		t_3,4{3,3,3,3,3,3,3,3} Quadritruncated 9-simplex								5670	1260
16		t_0,5{3,3,3,3,3,3,3,3} Pentellated 9-simplex								15750	1260
17		t_1,5{3,3,3,3,3,3,3,3} Bistericated 9-simplex								37800	3150
18		t_2,5{3,3,3,3,3,3,3,3} Triruncinated 9-simplex								44100	4200
19		t_3,5{3,3,3,3,3,3,3,3} Quadricantellated 9-simplex								25200	3150
20		t_0,6{3,3,3,3,3,3,3,3} Hexicated 9-simplex								10080	840
21		t_1,6{3,3,3,3,3,3,3,3} Bipentellated 9-simplex								31500	2520
22		t_2,6{3,3,3,3,3,3,3,3} Tristericated 9-simplex								50400	4200
23		t_0,7{3,3,3,3,3,3,3,3} Heptellated 9-simplex								3780	360
24		t_1,7{3,3,3,3,3,3,3,3} Bihexicated 9-simplex								15120	1260
25		t_0,8{3,3,3,3,3,3,3,3} Octellated 9-simplex								720	90
26		t_0,1,2{3,3,3,3,3,3,3,3} Cantitruncated 9-simplex								3240	720
27		t_0,1,3{3,3,3,3,3,3,3,3} Runcitruncated 9-simplex								18900	2520
28		t_0,2,3{3,3,3,3,3,3,3,3} Runcicantellated 9-simplex								12600	2520
29		t_1,2,3{3,3,3,3,3,3,3,3} Bicantitruncated 9-simplex								11340	2520
30		t_0,1,4{3,3,3,3,3,3,3,3} Steritruncated 9-simplex								47880	5040
31		t_0,2,4{3,3,3,3,3,3,3,3} Stericantellated 9-simplex								60480	7560
32		t_1,2,4{3,3,3,3,3,3,3,3} Biruncitruncated 9-simplex								52920	7560
33		t_0,3,4{3,3,3,3,3,3,3,3} Steriruncinated 9-simplex								27720	5040
34		t_1,3,4{3,3,3,3,3,3,3,3} Biruncicantellated 9-simplex								41580	7560
35		t_2,3,4{3,3,3,3,3,3,3,3} Tricantitruncated 9-simplex								22680	5040
36		t_0,1,5{3,3,3,3,3,3,3,3} Pentitruncated 9-simplex								66150	6300
37		t_0,2,5{3,3,3,3,3,3,3,3} Penticantellated 9-simplex								126000	12600
38		t_1,2,5{3,3,3,3,3,3,3,3} Bisteritruncated 9-simplex								107100	12600
39		t_0,3,5{3,3,3,3,3,3,3,3} Pentiruncinated 9-simplex								107100	12600
40		t_1,3,5{3,3,3,3,3,3,3,3} Bistericantellated 9-simplex								151200	18900
41		t_2,3,5{3,3,3,3,3,3,3,3} Triruncitruncated 9-simplex								81900	12600
42		t_0,4,5{3,3,3,3,3,3,3,3} Pentistericated 9-simplex								37800	6300
43		t_1,4,5{3,3,3,3,3,3,3,3} Bisteriruncinated 9-simplex								81900	12600
44		t_2,4,5{3,3,3,3,3,3,3,3} Triruncicantellated 9-simplex								75600	12600
45		t_3,4,5{3,3,3,3,3,3,3,3} Quadricantitruncated 9-simplex								28350	6300
46		t_0,1,6{3,3,3,3,3,3,3,3} Hexitruncated 9-simplex								52920	5040
47		t_0,2,6{3,3,3,3,3,3,3,3} Hexicantellated 9-simplex								138600	12600
48		t_1,2,6{3,3,3,3,3,3,3,3} Bipentitruncated 9-simplex								113400	12600
49		t_0,3,6{3,3,3,3,3,3,3,3} Hexiruncinated 9-simplex								176400	16800
50		t_1,3,6{3,3,3,3,3,3,3,3} Bipenticantellated 9-simplex								239400	25200
51		t_2,3,6{3,3,3,3,3,3,3,3} Tristeritruncated 9-simplex								126000	16800
52		t_0,4,6{3,3,3,3,3,3,3,3} Hexistericated 9-simplex								113400	12600
53		t_1,4,6{3,3,3,3,3,3,3,3} Bipentiruncinated 9-simplex								226800	25200
54		t_2,4,6{3,3,3,3,3,3,3,3} Tristericantellated 9-simplex								201600	25200
55		t_0,5,6{3,3,3,3,3,3,3,3} Hexipentellated 9-simplex								32760	5040
56		t_1,5,6{3,3,3,3,3,3,3,3} Bipentistericated 9-simplex								94500	12600
57		t_0,1,7{3,3,3,3,3,3,3,3} Heptitruncated 9-simplex								23940	2520
58		t_0,2,7{3,3,3,3,3,3,3,3} Hepticantellated 9-simplex								83160	7560
59		t_1,2,7{3,3,3,3,3,3,3,3} Bihexitruncated 9-simplex								64260	7560
60		t_0,3,7{3,3,3,3,3,3,3,3} Heptiruncinated 9-simplex								144900	12600
61		t_1,3,7{3,3,3,3,3,3,3,3} Bihexicantellated 9-simplex								189000	18900
62		t_0,4,7{3,3,3,3,3,3,3,3} Heptistericated 9-simplex								138600	12600
63		t_1,4,7{3,3,3,3,3,3,3,3} Bihexiruncinated 9-simplex								264600	25200
64		t_0,5,7{3,3,3,3,3,3,3,3} Heptipentellated 9-simplex								71820	7560
65		t_0,6,7{3,3,3,3,3,3,3,3} Heptihexicated 9-simplex								17640	2520
66		t_0,1,8{3,3,3,3,3,3,3,3} Octitruncated 9-simplex								5400	720
67		t_0,2,8{3,3,3,3,3,3,3,3} Octicantellated 9-simplex								25200	2520
68		t_0,3,8{3,3,3,3,3,3,3,3} Octiruncinated 9-simplex								57960	5040
69		t_0,4,8{3,3,3,3,3,3,3,3} Octistericated 9-simplex								75600	6300
70		t_0,1,2,3{3,3,3,3,3,3,3,3} Runcicantitruncated 9-simplex								22680	5040
71		t_0,1,2,4{3,3,3,3,3,3,3,3} Stericantitruncated 9-simplex								105840	15120
72		t_0,1,3,4{3,3,3,3,3,3,3,3} Steriruncitruncated 9-simplex								75600	15120
73		t_0,2,3,4{3,3,3,3,3,3,3,3} Steriruncicantellated 9-simplex								75600	15120
74		t_1,2,3,4{3,3,3,3,3,3,3,3} Biruncicantitruncated 9-simplex								68040	15120
75		t_0,1,2,5{3,3,3,3,3,3,3,3} Penticantitruncated 9-simplex								214200	25200
76		t_0,1,3,5{3,3,3,3,3,3,3,3} Pentiruncitruncated 9-simplex								283500	37800
77		t_0,2,3,5{3,3,3,3,3,3,3,3} Pentiruncicantellated 9-simplex								264600	37800
78		t_1,2,3,5{3,3,3,3,3,3,3,3} Bistericantitruncated 9-simplex								245700	37800
79		t_0,1,4,5{3,3,3,3,3,3,3,3} Pentisteritruncated 9-simplex								138600	25200
80		t_0,2,4,5{3,3,3,3,3,3,3,3} Pentistericantellated 9-simplex								226800	37800
81		t_1,2,4,5{3,3,3,3,3,3,3,3} Bisteriruncitruncated 9-simplex								189000	37800
82		t_0,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncinated 9-simplex								138600	25200
83		t_1,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantellated 9-simplex								207900	37800
84		t_2,3,4,5{3,3,3,3,3,3,3,3} Triruncicantitruncated 9-simplex								113400	25200
85		t_0,1,2,6{3,3,3,3,3,3,3,3} Hexicantitruncated 9-simplex								226800	25200
86		t_0,1,3,6{3,3,3,3,3,3,3,3} Hexiruncitruncated 9-simplex								453600	50400
87		t_0,2,3,6{3,3,3,3,3,3,3,3} Hexiruncicantellated 9-simplex								403200	50400
88		t_1,2,3,6{3,3,3,3,3,3,3,3} Bipenticantitruncated 9-simplex								378000	50400
89		t_0,1,4,6{3,3,3,3,3,3,3,3} Hexisteritruncated 9-simplex								403200	50400
90		t_0,2,4,6{3,3,3,3,3,3,3,3} Hexistericantellated 9-simplex								604800	75600
91		t_1,2,4,6{3,3,3,3,3,3,3,3} Bipentiruncitruncated 9-simplex								529200	75600
92		t_0,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncinated 9-simplex								352800	50400
93		t_1,3,4,6{3,3,3,3,3,3,3,3} Bipentiruncicantellated 9-simplex								529200	75600
94		t_2,3,4,6{3,3,3,3,3,3,3,3} Tristericantitruncated 9-simplex								302400	50400
95		t_0,1,5,6{3,3,3,3,3,3,3,3} Hexipentitruncated 9-simplex								151200	25200
96		t_0,2,5,6{3,3,3,3,3,3,3,3} Hexipenticantellated 9-simplex								352800	50400
97		t_1,2,5,6{3,3,3,3,3,3,3,3} Bipentisteritruncated 9-simplex								277200	50400
98		t_0,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncinated 9-simplex								352800	50400
99		t_1,3,5,6{3,3,3,3,3,3,3,3} Bipentistericantellated 9-simplex								491400	75600
100		t_2,3,5,6{3,3,3,3,3,3,3,3} Tristeriruncitruncated 9-simplex								252000	50400
101		t_0,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericated 9-simplex								151200	25200
102		t_1,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncinated 9-simplex								327600	50400
103		t_0,1,2,7{3,3,3,3,3,3,3,3} Hepticantitruncated 9-simplex								128520	15120
104		t_0,1,3,7{3,3,3,3,3,3,3,3} Heptiruncitruncated 9-simplex								359100	37800
105		t_0,2,3,7{3,3,3,3,3,3,3,3} Heptiruncicantellated 9-simplex								302400	37800
106		t_1,2,3,7{3,3,3,3,3,3,3,3} Bihexicantitruncated 9-simplex								283500	37800
107		t_0,1,4,7{3,3,3,3,3,3,3,3} Heptisteritruncated 9-simplex								478800	50400
108		t_0,2,4,7{3,3,3,3,3,3,3,3} Heptistericantellated 9-simplex								680400	75600
109		t_1,2,4,7{3,3,3,3,3,3,3,3} Bihexiruncitruncated 9-simplex								604800	75600
110		t_0,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncinated 9-simplex								378000	50400
111		t_1,3,4,7{3,3,3,3,3,3,3,3} Bihexiruncicantellated 9-simplex								567000	75600
112		t_0,1,5,7{3,3,3,3,3,3,3,3} Heptipentitruncated 9-simplex								321300	37800
113		t_0,2,5,7{3,3,3,3,3,3,3,3} Heptipenticantellated 9-simplex								680400	75600
114		t_1,2,5,7{3,3,3,3,3,3,3,3} Bihexisteritruncated 9-simplex								567000	75600
115		t_0,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncinated 9-simplex								642600	75600
116		t_1,3,5,7{3,3,3,3,3,3,3,3} Bihexistericantellated 9-simplex								907200	113400
117		t_0,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericated 9-simplex								264600	37800
118		t_0,1,6,7{3,3,3,3,3,3,3,3} Heptihexitruncated 9-simplex								98280	15120
119		t_0,2,6,7{3,3,3,3,3,3,3,3} Heptihexicantellated 9-simplex								302400	37800
120		t_1,2,6,7{3,3,3,3,3,3,3,3} Bihexipentitruncated 9-simplex								226800	37800
121		t_0,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncinated 9-simplex								428400	50400
122		t_0,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericated 9-simplex								302400	37800
123		t_0,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentellated 9-simplex								98280	15120
124		t_0,1,2,8{3,3,3,3,3,3,3,3} Octicantitruncated 9-simplex								35280	5040
125		t_0,1,3,8{3,3,3,3,3,3,3,3} Octiruncitruncated 9-simplex								136080	15120
126		t_0,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantellated 9-simplex								105840	15120
127		t_0,1,4,8{3,3,3,3,3,3,3,3} Octisteritruncated 9-simplex								252000	25200
128		t_0,2,4,8{3,3,3,3,3,3,3,3} Octistericantellated 9-simplex								340200	37800
129		t_0,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncinated 9-simplex								176400	25200
130		t_0,1,5,8{3,3,3,3,3,3,3,3} Octipentitruncated 9-simplex								252000	25200
131		t_0,2,5,8{3,3,3,3,3,3,3,3} Octipenticantellated 9-simplex								504000	50400
132		t_0,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncinated 9-simplex								453600	50400
133		t_0,1,6,8{3,3,3,3,3,3,3,3} Octihexitruncated 9-simplex								136080	15120
134		t_0,2,6,8{3,3,3,3,3,3,3,3} Octihexicantellated 9-simplex								378000	37800
135		t_0,1,7,8{3,3,3,3,3,3,3,3} Octiheptitruncated 9-simplex								35280	5040
136		t_0,1,2,3,4{3,3,3,3,3,3,3,3} Steriruncicantitruncated 9-simplex								136080	30240
137		t_0,1,2,3,5{3,3,3,3,3,3,3,3} Pentiruncicantitruncated 9-simplex								491400	75600
138		t_0,1,2,4,5{3,3,3,3,3,3,3,3} Pentistericantitruncated 9-simplex								378000	75600
139		t_0,1,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncitruncated 9-simplex								378000	75600
140		t_0,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantellated 9-simplex								378000	75600
141		t_1,2,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantitruncated 9-simplex								340200	75600
142		t_0,1,2,3,6{3,3,3,3,3,3,3,3} Hexiruncicantitruncated 9-simplex								756000	100800
143		t_0,1,2,4,6{3,3,3,3,3,3,3,3} Hexistericantitruncated 9-simplex								1058400	151200
144		t_0,1,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncitruncated 9-simplex								982800	151200
145		t_0,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantellated 9-simplex								982800	151200
146		t_1,2,3,4,6{3,3,3,3,3,3,3,3} Bipentiruncicantitruncated 9-simplex								907200	151200
147		t_0,1,2,5,6{3,3,3,3,3,3,3,3} Hexipenticantitruncated 9-simplex								554400	100800
148		t_0,1,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncitruncated 9-simplex								907200	151200
149		t_0,2,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncicantellated 9-simplex								831600	151200
150		t_1,2,3,5,6{3,3,3,3,3,3,3,3} Bipentistericantitruncated 9-simplex								756000	151200
151		t_0,1,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteritruncated 9-simplex								554400	100800
152		t_0,2,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericantellated 9-simplex								907200	151200
153		t_1,2,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncitruncated 9-simplex								756000	151200
154		t_0,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncinated 9-simplex								554400	100800
155		t_1,3,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncicantellated 9-simplex								831600	151200
156		t_2,3,4,5,6{3,3,3,3,3,3,3,3} Tristeriruncicantitruncated 9-simplex								453600	100800
157		t_0,1,2,3,7{3,3,3,3,3,3,3,3} Heptiruncicantitruncated 9-simplex								567000	75600
158		t_0,1,2,4,7{3,3,3,3,3,3,3,3} Heptistericantitruncated 9-simplex								1209600	151200
159		t_0,1,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncitruncated 9-simplex								1058400	151200
160		t_0,2,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncicantellated 9-simplex								1058400	151200
161		t_1,2,3,4,7{3,3,3,3,3,3,3,3} Bihexiruncicantitruncated 9-simplex								982800	151200
162		t_0,1,2,5,7{3,3,3,3,3,3,3,3} Heptipenticantitruncated 9-simplex								1134000	151200
163		t_0,1,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncitruncated 9-simplex								1701000	226800
164		t_0,2,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncicantellated 9-simplex								1587600	226800
165		t_1,2,3,5,7{3,3,3,3,3,3,3,3} Bihexistericantitruncated 9-simplex								1474200	226800
166		t_0,1,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteritruncated 9-simplex								982800	151200
167		t_0,2,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericantellated 9-simplex								1587600	226800
168		t_1,2,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncitruncated 9-simplex								1360800	226800
169		t_0,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncinated 9-simplex								982800	151200
170		t_1,3,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncicantellated 9-simplex								1474200	226800
171		t_0,1,2,6,7{3,3,3,3,3,3,3,3} Heptihexicantitruncated 9-simplex								453600	75600
172		t_0,1,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncitruncated 9-simplex								1058400	151200
173		t_0,2,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncicantellated 9-simplex								907200	151200
174		t_1,2,3,6,7{3,3,3,3,3,3,3,3} Bihexipenticantitruncated 9-simplex								831600	151200
175		t_0,1,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteritruncated 9-simplex								1058400	151200
176		t_0,2,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericantellated 9-simplex								1587600	226800
177		t_1,2,4,6,7{3,3,3,3,3,3,3,3} Bihexipentiruncitruncated 9-simplex								1360800	226800
178		t_0,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncinated 9-simplex								907200	151200
179		t_0,1,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentitruncated 9-simplex								453600	75600
180		t_0,2,5,6,7{3,3,3,3,3,3,3,3} Heptihexipenticantellated 9-simplex								1058400	151200
181		t_0,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncinated 9-simplex								1058400	151200
182		t_0,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentistericated 9-simplex								453600	75600
183		t_0,1,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantitruncated 9-simplex								196560	30240
184		t_0,1,2,4,8{3,3,3,3,3,3,3,3} Octistericantitruncated 9-simplex								604800	75600
185		t_0,1,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncitruncated 9-simplex								491400	75600
186		t_0,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantellated 9-simplex								491400	75600
187		t_0,1,2,5,8{3,3,3,3,3,3,3,3} Octipenticantitruncated 9-simplex								856800	100800
188		t_0,1,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncitruncated 9-simplex								1209600	151200
189		t_0,2,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncicantellated 9-simplex								1134000	151200
190		t_0,1,4,5,8{3,3,3,3,3,3,3,3} Octipentisteritruncated 9-simplex								655200	100800
191		t_0,2,4,5,8{3,3,3,3,3,3,3,3} Octipentistericantellated 9-simplex								1058400	151200
192		t_0,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncinated 9-simplex								655200	100800
193		t_0,1,2,6,8{3,3,3,3,3,3,3,3} Octihexicantitruncated 9-simplex								604800	75600
194		t_0,1,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncitruncated 9-simplex								1285200	151200
195		t_0,2,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncicantellated 9-simplex								1134000	151200
196		t_0,1,4,6,8{3,3,3,3,3,3,3,3} Octihexisteritruncated 9-simplex								1209600	151200
197		t_0,2,4,6,8{3,3,3,3,3,3,3,3} Octihexistericantellated 9-simplex								1814400	226800
198		t_0,1,5,6,8{3,3,3,3,3,3,3,3} Octihexipentitruncated 9-simplex								491400	75600
199		t_0,1,2,7,8{3,3,3,3,3,3,3,3} Octihepticantitruncated 9-simplex								196560	30240
200		t_0,1,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncitruncated 9-simplex								604800	75600
201		t_0,1,4,7,8{3,3,3,3,3,3,3,3} Octiheptisteritruncated 9-simplex								856800	100800
202		t_0,1,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantitruncated 9-simplex								680400	151200
203		t_0,1,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantitruncated 9-simplex								1814400	302400
204		t_0,1,2,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncicantitruncated 9-simplex								1512000	302400
205		t_0,1,2,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericantitruncated 9-simplex								1512000	302400
206		t_0,1,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncitruncated 9-simplex								1512000	302400
207		t_0,2,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncicantellated 9-simplex								1512000	302400
208		t_1,2,3,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncicantitruncated 9-simplex								1360800	302400
209		t_0,1,2,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncicantitruncated 9-simplex								1965600	302400
210		t_0,1,2,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncicantitruncated 9-simplex								2948400	453600
211		t_0,1,2,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericantitruncated 9-simplex								2721600	453600
212		t_0,1,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncitruncated 9-simplex								2721600	453600
213		t_0,2,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncicantellated 9-simplex								2721600	453600
214		t_1,2,3,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncicantitruncated 9-simplex								2494800	453600
215		t_0,1,2,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncicantitruncated 9-simplex								1663200	302400
216		t_0,1,2,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericantitruncated 9-simplex								2721600	453600
217		t_0,1,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncitruncated 9-simplex								2494800	453600
218		t_0,2,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncicantellated 9-simplex								2494800	453600
219		t_1,2,3,4,6,7{3,3,3,3,3,3,3,3} Bihexipentiruncicantitruncated 9-simplex								2268000	453600
220		t_0,1,2,5,6,7{3,3,3,3,3,3,3,3} Heptihexipenticantitruncated 9-simplex								1663200	302400
221		t_0,1,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncitruncated 9-simplex								2721600	453600
222		t_0,2,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncicantellated 9-simplex								2494800	453600
223		t_1,2,3,5,6,7{3,3,3,3,3,3,3,3} Bihexipentistericantitruncated 9-simplex								2268000	453600
224		t_0,1,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteritruncated 9-simplex								1663200	302400
225		t_0,2,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentistericantellated 9-simplex								2721600	453600
226		t_0,3,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteriruncinated 9-simplex								1663200	302400
227		t_0,1,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantitruncated 9-simplex								907200	151200
228		t_0,1,2,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncicantitruncated 9-simplex								2116800	302400
229		t_0,1,2,4,5,8{3,3,3,3,3,3,3,3} Octipentistericantitruncated 9-simplex								1814400	302400
230		t_0,1,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncitruncated 9-simplex								1814400	302400
231		t_0,2,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncicantellated 9-simplex								1814400	302400
232		t_0,1,2,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncicantitruncated 9-simplex								2116800	302400
233		t_0,1,2,4,6,8{3,3,3,3,3,3,3,3} Octihexistericantitruncated 9-simplex								3175200	453600
234		t_0,1,3,4,6,8{3,3,3,3,3,3,3,3} Octihexisteriruncitruncated 9-simplex								2948400	453600
235		t_0,2,3,4,6,8{3,3,3,3,3,3,3,3} Octihexisteriruncicantellated 9-simplex								2948400	453600
236		t_0,1,2,5,6,8{3,3,3,3,3,3,3,3} Octihexipenticantitruncated 9-simplex								1814400	302400
237		t_0,1,3,5,6,8{3,3,3,3,3,3,3,3} Octihexipentiruncitruncated 9-simplex								2948400	453600
238		t_0,2,3,5,6,8{3,3,3,3,3,3,3,3} Octihexipentiruncicantellated 9-simplex								2721600	453600
239		t_0,1,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentisteritruncated 9-simplex								1814400	302400
240		t_0,1,2,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncicantitruncated 9-simplex								907200	151200
241		t_0,1,2,4,7,8{3,3,3,3,3,3,3,3} Octiheptistericantitruncated 9-simplex								2116800	302400
242		t_0,1,3,4,7,8{3,3,3,3,3,3,3,3} Octiheptisteriruncitruncated 9-simplex								1814400	302400
243		t_0,1,2,5,7,8{3,3,3,3,3,3,3,3} Octiheptipenticantitruncated 9-simplex								2116800	302400
244		t_0,1,3,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentiruncitruncated 9-simplex								3175200	453600
245		t_0,1,2,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexicantitruncated 9-simplex								907200	151200
246		t_{0,1,2,3,4,5,6}{3,3,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 9-simplex								2721600	604800
247		t_{0,1,2,3,4,5,7}{3,3,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 9-simplex								4989600	907200
248		t_{0,1,2,3,4,6,7}{3,3,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 9-simplex								4536000	907200
249		t_{0,1,2,3,5,6,7}{3,3,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 9-simplex								4536000	907200
250		t_{0,1,2,4,5,6,7}{3,3,3,3,3,3,3,3} Heptihexipentistericantitruncated 9-simplex								4536000	907200
251		t_{0,1,3,4,5,6,7}{3,3,3,3,3,3,3,3} Heptihexipentisteriruncitruncated 9-simplex								4536000	907200
252		t_{0,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Heptihexipentisteriruncicantellated 9-simplex								4536000	907200
253		t_{1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Bihexipentisteriruncicantitruncated 9-simplex								4082400	907200
254		t_{0,1,2,3,4,5,8}{3,3,3,3,3,3,3,3} Octipentisteriruncicantitruncated 9-simplex								3326400	604800
255		t_{0,1,2,3,4,6,8}{3,3,3,3,3,3,3,3} Octihexisteriruncicantitruncated 9-simplex								5443200	907200
256		t_{0,1,2,3,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentiruncicantitruncated 9-simplex								4989600	907200
257		t_{0,1,2,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentistericantitruncated 9-simplex								4989600	907200
258		t_{0,1,3,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentisteriruncitruncated 9-simplex								4989600	907200
259		t_{0,2,3,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantellated 9-simplex								4989600	907200
260		t_{0,1,2,3,4,7,8}{3,3,3,3,3,3,3,3} Octiheptisteriruncicantitruncated 9-simplex								3326400	604800
261		t_{0,1,2,3,5,7,8}{3,3,3,3,3,3,3,3} Octiheptipentiruncicantitruncated 9-simplex								5443200	907200
262		t_{0,1,2,4,5,7,8}{3,3,3,3,3,3,3,3} Octiheptipentistericantitruncated 9-simplex								4989600	907200
263		t_{0,1,3,4,5,7,8}{3,3,3,3,3,3,3,3} Octiheptipentisteriruncitruncated 9-simplex								4989600	907200
264		t_{0,1,2,3,6,7,8}{3,3,3,3,3,3,3,3} Octiheptihexiruncicantitruncated 9-simplex								3326400	604800
265		t_{0,1,2,4,6,7,8}{3,3,3,3,3,3,3,3} Octiheptihexistericantitruncated 9-simplex								5443200	907200
266		t_{0,1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Heptihexipentisteriruncicantitruncated 9-simplex								8164800	1814400
267		t_{0,1,2,3,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantitruncated 9-simplex								9072000	1814400
268		t_{0,1,2,3,4,5,7,8}{3,3,3,3,3,3,3,3} Octiheptipentisteriruncicantitruncated 9-simplex								9072000	1814400
269		t_{0,1,2,3,4,6,7,8}{3,3,3,3,3,3,3,3} Octiheptihexisteriruncicantitruncated 9-simplex								9072000	1814400
270		t_{0,1,2,3,5,6,7,8}{3,3,3,3,3,3,3,3} Octiheptihexipentiruncicantitruncated 9-simplex								9072000	1814400
271		t_{0,1,2,3,4,5,6,7,8}{3,3,3,3,3,3,3,3} Omnitruncated 9-simplex								16329600	3628800

The B₉ family

There are 511 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings.

Eleven cases are shown below: Nine rectified forms and 2 truncations. Bowers-style acronym names are given in parentheses for cross-referencing. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	Element counts
#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	8-faces	7-faces	6-faces	5-faces	4-faces	Cells	Faces	Edges	Vertices
1		t₀{4,3,3,3,3,3,3,3} 9-cube (enne)	18	144	672	2016	4032	5376	4608	2304	512
2		t_0,1{4,3,3,3,3,3,3,3} Truncated 9-cube (ten)								2304	4608
3		t₁{4,3,3,3,3,3,3,3} Rectified 9-cube (ren)								18432	2304
4		t₂{4,3,3,3,3,3,3,3} Birectified 9-cube (barn)								64512	4608
5		t₃{4,3,3,3,3,3,3,3} Trirectified 9-cube (tarn)								96768	5376
6		t₄{4,3,3,3,3,3,3,3} Quadrirectified 9-cube (nav) (Quadrirectified 9-orthoplex)								80640	4032
7		t₃{3,3,3,3,3,3,3,4} Trirectified 9-orthoplex (tarv)								40320	2016
8		t₂{3,3,3,3,3,3,3,4} Birectified 9-orthoplex (brav)								12096	672
9		t₁{3,3,3,3,3,3,3,4} Rectified 9-orthoplex (riv)								2016	144
10		t_0,1{3,3,3,3,3,3,3,4} Truncated 9-orthoplex (tiv)								2160	288
11		t₀{3,3,3,3,3,3,3,4} 9-orthoplex (vee)	512	2304	4608	5376	4032	2016	672	144	18

The D₉ family

The D₉ family has symmetry of order 92,897,280 (9 factorial × 2⁸).

This family has 3×128−1=383 Wythoffian uniform polytopes, generated by marking one or more nodes of the D₉ Coxeter-Dynkin diagram. Of these, 255 (2×128−1) are repeated from the B₉ family and 128 are unique to this family, with the eight 1 or 2 ringed forms listed below. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Coxeter plane graphs											Coxeter-Dynkin diagram Schläfli symbol	Base point (Alternately signed)	Element counts									Circumrad
#	B₉	D₉	D₈	D₇	D₆	D₅	D₄	D₃	A₇	A₅	A₃	Coxeter-Dynkin diagram Schläfli symbol	Base point (Alternately signed)	8	7	6	5	4	3	2	1	0	Circumrad
1		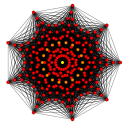								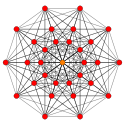		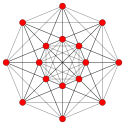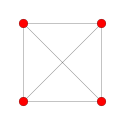9-demicube (henne)	(1,1,1,1,1,1,1,1,1)	274	2448	9888	23520	36288	37632	21404	4608	256	1.0606601
2												Truncated 9-demicube (thenne)	(1,1,3,3,3,3,3,3,3)								69120	9216	2.8504384
3												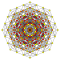Cantellated 9-demicube	(1,1,1,3,3,3,3,3,3)								225792	21504	2.6692696
4												Runcinated 9-demicube	(1,1,1,1,3,3,3,3,3)								419328	32256	2.4748735
5												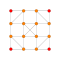Stericated 9-demicube	(1,1,1,1,1,3,3,3,3)								483840	32256	2.2638462
6												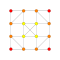Pentellated 9-demicube	(1,1,1,1,1,1,3,3,3)								354816	21504	2.0310094
7												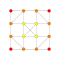Hexicated 9-demicube	(1,1,1,1,1,1,1,3,3)								161280	9216	1.7677668
8										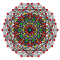		Heptellated 9-demicube	(1,1,1,1,1,1,1,1,3)								41472	2304	1.4577379

Regular and uniform honeycombs

Coxeter-Dynkin diagram correspondences between families and higher symmetry within diagrams. Nodes of the same color in each row represent identical mirrors. Black nodes are not active in the correspondence.

There are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 8-space:

#	Coxeter group		Forms
1	${{\tilde {A}}}_{8}$	[3^[9]]	45
2	${{\tilde {C}}}_{8}$	[4,3⁶,4]	271
3	${{\tilde {B}}}_{8}$	h[4,3⁶,4] [4,3⁵,3^1,1]	383 (128 new)
4	${{\tilde {D}}}_{8}$	q[4,3⁶,4] [3^1,1,3⁴,3^1,1]	155 (15 new)
5	${\tilde {E}}_{8}$	[3^5,2,1]	511

Regular and uniform tessellations include:

${{\tilde {A}}}_{8}$ 45 uniquely ringed forms
- 8-simplex honeycomb: {3^[9]}
${{\tilde {C}}}_{8}$ 271 uniquely ringed forms
- Regular 8-cube honeycomb: {4,3⁶,4},
${{\tilde {B}}}_{8}$ : 383 uniquely ringed forms, 255 shared with ${{\tilde {C}}}_{8}$ , 128 new
- 8-demicube honeycomb: h{4,3⁶,4} or {3^1,1,3⁵,4}, or
${{\tilde {D}}}_{8}$ , [3^1,1,3⁴,3^1,1]: 155 unique ring permutations, and 15 are new, the first, , Coxeter called a quarter 8-cubic honeycomb, representing as q{4,3⁶,4}, or qδ₉.
${\tilde {E}}_{8}$ 511 forms

Regular and uniform hyperbolic honeycombs

There are no compact hyperbolic Coxeter groups of rank 9, groups that can generate honeycombs with all finite facets, and a finite vertex figure. However, there are 4 noncompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 8-space as permutations of rings of the Coxeter diagrams.

${\bar {P}}_{8}$ = [3,3^[8]]:	${\bar {Q}}_{8}$ = [3^1,1,3³,3^2,1]:	${\bar {S}}_{8}$ = [4,3⁴,3^2,1]:	${\bar {T}}_{8}$ = [3^4,3,1]:

References

1 2 3 Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.

T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Klitzing, Richard. "9D uniform polytopes (polyyotta)".

External links

Polytope names
Polytopes of Various Dimensions, Jonathan Bowers
Multi-dimensional Glossary
Glossary for hyperspace, George Olshevsky.

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / E₉ / E₁₀ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9)
Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
Uniform tiling	{3^[3]}	δ₃	hδ₃	qδ₃	Hexagonal
Uniform convex honeycomb	{3^[4]}	δ₄	hδ₄	qδ₄
Uniform 5-honeycomb	{3^[5]}	δ₅	hδ₅	qδ₅	24-cell honeycomb
Uniform 6-honeycomb	{3^[6]}	δ₆	hδ₆	qδ₆
Uniform 7-honeycomb	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
Uniform 8-honeycomb	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
Uniform 9-honeycomb	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
Uniform 10-honeycomb	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
Uniform n-honeycomb	{3^[n]}	δ_n	hδ_n	qδ_n	1_k2 • 2_k1 • k₂₁

This article is issued from Wikipedia - version of the 6/30/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.