Uniform 1 k2 polytope
In geometry, 1k2 polytope is a uniform polytope in n-dimensions (n = k+4) constructed from the En Coxeter group. The family was named by their Coxeter symbol 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence. It can be named by an extended Schläfli symbol {3,3k,2}.
Family members
The family starts uniquely as 6-polytopes, but can be extended backwards to include the 5-demicube (demipenteract) in 5-dimensions, and the 4-simplex (5-cell) in 4-dimensions.
Each polytope is constructed from 1k-1,2 and (n-1)-demicube facets. Each has a vertex figure of a {31,n-2,2} polytope is a birectified n-simplex, t2{3n}.
The sequence ends with k=6 (n=10), as an infinite tessellation of 9-dimensional hyperbolic space.
The complete family of 1k2 polytope polytopes are:
- 5-cell: 102, (5 tetrahedral cells)
- 112 polytope, (16 5-cell, and 10 16-cell facets)
- 122 polytope, (54 demipenteract facets)
- 132 polytope, (56 122 and 126 demihexeract facets)
- 142 polytope, (240 132 and 2160 demihepteract facets)
- 152 honeycomb, tessellates Euclidean 8-space (∞ 142 and ∞ demiocteract facets)
- 162 honeycomb, tessellates hyperbolic 9-space (∞ 152 and ∞ demienneract facets)
Elements
| n | 1k2 | Petrie polygon projection |
Name Coxeter-Dynkin diagram |
Facets | Elements | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1k-1,2 | (n-1)-demicube | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | ||||
| 4 | 102 | 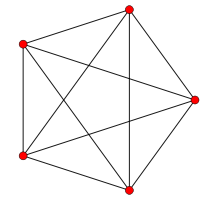 |
120 |
-- | 5 110 |
5 | 10 | 10 |
5 |
||||
| 5 | 112 |  |
121 |
16 120 |
10 111 |
16 | 80 | 160 |
120 |
26 |
|||
| 6 | 122 |  |
122 |
27 112 |
27 121 |
72 | 720 | 2160 |
2160 |
702 |
54 |
||
| 7 | 132 | 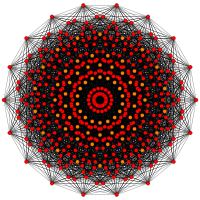 |
132 |
56 122 |
126 131 |
576 | 10080 | 40320 |
50400 |
23688 |
4284 |
182 |
|
| 8 | 142 |  |
142 |
240 132 |
2160 141 |
17280 | 483840 | 2419200 |
3628800 |
2298240 |
725760 |
106080 |
2400 |
| 9 | 152 | 152 (8-space tessellation) |
∞ 142 |
∞ 151 |
∞ | ||||||||
| 10 | 162 | 162 (9-space hyperbolic tessellation) |
∞ 152 |
∞ 161 |
∞ | ||||||||
See also
- k21 polytope family
- 2k1 polytope family
References
- Alicia Boole Stott Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- Stott, A. B. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam 11, 3-24, 1910.
- Alicia Boole Stott, "Geometrical deduction of semiregular from regular polytopes and space fillings," Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, (eerste sectie), Vol. 11, No. 1, pp. 1–24 plus 3 plates, 1910.
- Stott, A. B. 1910. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam
- Schoute, P. H., Analytical treatment of the polytopes regularly derived from the regular polytopes, Ver. der Koninklijke Akad. van Wetenschappen te Amsterdam (eerstie sectie), vol 11.5, 1913.
- H. S. M. Coxeter: Regular and Semi-Regular Polytopes, Part I, Mathematische Zeitschrift, Springer, Berlin, 1940
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part II, Mathematische Zeitschrift, Springer, Berlin, 1985
- H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part III, Mathematische Zeitschrift, Springer, Berlin, 1988
External links
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
| Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9) | |||||
|---|---|---|---|---|---|
| Family | / / | ||||
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform 10-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |