Johnson solid

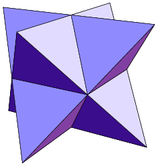

In geometry, a Johnson solid is a strictly convex polyhedron, which is not uniform (i.e., not a Platonic solid, Archimedean solid, prism or antiprism), and each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1); it has 1 square face and 4 triangular faces.
As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid (J2) is an example that actually has a degree-5 vertex.
Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the faces of Johnson solids always have 3, 4, 5, 6, 8, or 10 sides.
In 1966, Norman Johnson published a list which included all 92 solids, and gave them their names and numbers. He did not prove that there were only 92, but he did conjecture that there were no others. Victor Zalgaller in 1969 proved that Johnson's list was complete.
Of the Johnson solids, the elongated square gyrobicupola (J37), also called the pseudorhombicuboctahedron,[1] is unique in being locally vertex-uniform: there are 4 faces at each vertex, and their arrangement is always the same: 3 squares and 1 triangle. However, it is not vertex-transitive, as it has different isometry at different vertices, making it a Johnson solid rather than an Archimedean solid.
Names
The names are listed below and are more descriptive than they sound. Most of the Johnson solids can be constructed from the first few (pyramids, cupolae, and rotunda), together with the Platonic and Archimedean solids, prisms, and antiprisms.
- Bi- means that two copies of the solid in question are joined base-to-base. For cupolae and rotundae, they can be joined so that like faces (ortho-) or unlike faces (gyro-) meet. In this nomenclature, an octahedron would be a square bipyramid, a cuboctahedron would be a triangular gyrobicupola, and an icosidodecahedron would be a pentagonal gyrobirotunda.
- Elongated means that a prism has been joined to the base of the solid in question or between the bases of the solids in question. A rhombicuboctahedron would be an elongated square orthobicupola.
- Gyroelongated means that an antiprism has been joined to the base of the solid in question or between the bases of the solids in question. An icosahedron would be a gyroelongated pentagonal bipyramid.
- Augmented means that a pyramid or cupola has been joined to a face of the solid in question.
- Diminished means that a pyramid or cupola has been removed from the solid in question.
- Gyrate means that a cupola on the solid in question has been rotated so that different edges match up, as in the difference between ortho- and gyrobicupolae.
The last three operations — augmentation, diminution, and gyration — can be performed more than once on a large enough solid. We add bi- to the name of the operation to indicate that it has been performed twice. (A bigyrate solid has had two of its cupolae rotated.) We add tri- to indicate that it has been performed three times. (A tridiminished solid has had three of its pyramids or cupolae removed.)
Sometimes, bi- alone is not specific enough. We must distinguish between a solid that has had two parallel faces altered and one that has had two oblique faces altered. When the faces altered are parallel, we add para- to the name of the operation. (A parabiaugmented solid has had two parallel faces augmented.) When they are not, we add meta- to the name of the operation. (A metabiaugmented solid has had 2 oblique faces augmented.)
The last few Johnson solids have names based on certain polygon complexes that they are assembled from. These names are defined by Johnson as follows:[2]
- If we define a lune as a complex of two triangles attached to opposite sides of a square, the prefix spheno- refers to a wedgelike complex formed by two adjacent lunes. The prefix dispheno- denotes two such complexes, while hebespheno- indicates a blunter complex of two lunes separated by a third lune. The suffix -corona refers to a crownlike complex of eight triangles, and -megacorona, to a larger such complex of 12 triangles. The suffix -cingulum indicates a belt of 12 triangles.
Enumeration
Pyramids
The first two Johnson solids, J1 and J2, are pyramids. The triangular pyramid is the regular tetrahedron, so it is not a Johnson solid.
| Regular | J1 | J2 |
|---|---|---|
| Triangular pyramid (Tetrahedron) |
Square pyramid | Pentagonal pyramid |
 |
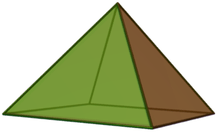 |
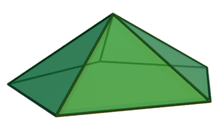 |
 |
 |
 |
Cupolæ and rotunda
The next four Johnson solids are three cupolae and one rotunda. They represent sections of uniform polyhedra.
| Cupola | Rotunda | |||
|---|---|---|---|---|
| Uniform | J3 | J4 | J5 | J6 |
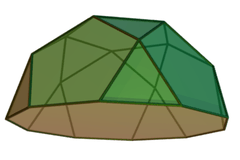
| Triangular prism | Triangular cupola | Square cupola | Pentagonal cupola | Pentagonal rotunda |
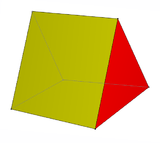 |
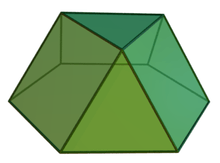 |
 |
 |
 |
 |
 |
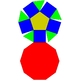 |
 | |
| Related uniform polyhedra | ||||
| Cuboctahedron | Rhombicuboctahedron | Rhombicosidodecahedron | Icosidodecahedron | |
 |
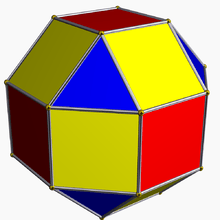 |
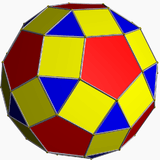 |
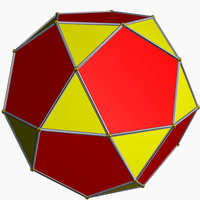 | |
Elongated and gyroelongated pyramids
The next five Johnson solids are elongated and gyroelongated pyramids. These represent the composite or augmentation of two polyhedra. In the gyroelongated triangular pyramid, three pairs of adjacent triangles are coplanar and form non-square rhombi, so it is not a Johnson solid.
| Elongated pyramids (or augmented prisms) |
Gyroelongated pyramids (or augmented antiprisms) | ||||
|---|---|---|---|---|---|
| J7 | J8 | J9 | Coplanar | J10 | J11 |
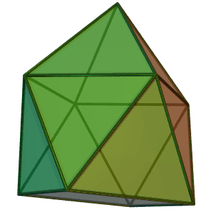
| Elongated triangular pyramid | Elongated square pyramid | Elongated pentagonal pyramid | Gyroelongated triangular pyramid | Gyroelongated square pyramid | Gyroelongated pentagonal pyramid |
| Augmented triangular prism | Augmented cube | Augmented pentagonal prism | Augmented octahedron | Augmented square antiprism | Augmented pentagonal antiprism |
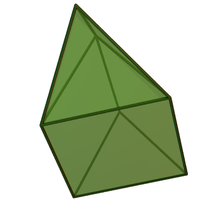 |
 |
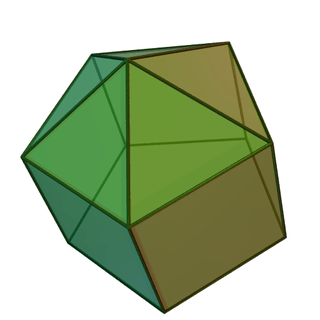 |
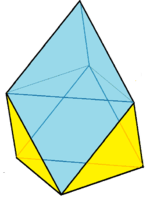 |
 |
 |
 |
 |
 |
|
 |
 |
| Augmented from polyhedra | |||||
| tetrahedron triangular prism |
square pyramid cube |
pentagonal pyramid pentagonal prism |
tetrahedron octahedron |
square pyramid square antiprism |
pentagonal pyramid pentagonal antiprism |
Bipyramids
The next six Johnson solids are bipyramids, elongated bipyramids, and gyroelongated bipyramids:
| Bipyramids | Elongated bipyramids | Gyroelongated bipyramids | ||||||
|---|---|---|---|---|---|---|---|---|
| J12 | Regular | J13 | J14 | J15 | J16 | Coplanar | J17 | Regular |
| Triangular bipyramid | Square bipyramid (octahedron) |
Pentagonal bipyramid | Elongated triangular bipyramid | Elongated square bipyramid | Elongated pentagonal bipyramid | Gyroelongated triangular bipyramid (rhombohedron) |
Gyroelongated square bipyramid | Gyroelongated pentagonal bipyramid (icosahedron) |
 |
 |
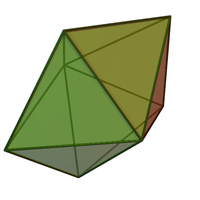 |
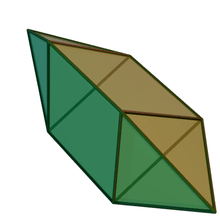 |
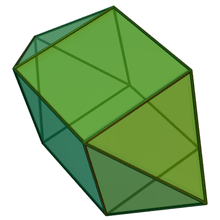 |
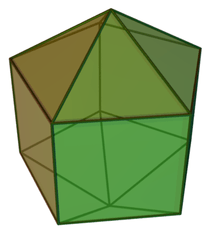 |
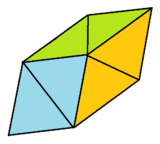 |
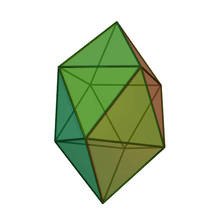 |
 |
 |
 |
 |
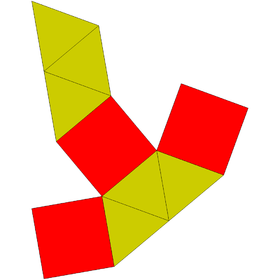 |
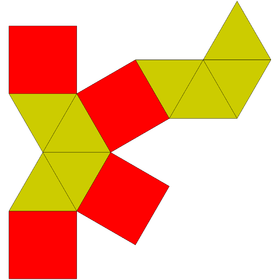 |
 |
 |
| |
| Augmented from polyhedra | ||||||||
| tetrahedron | square pyramid | pentagonal pyramid | tetrahedron triangular prism |
square pyramid cube |
pentagonal pyramid pentagonal prism |
tetrahedron Octahedron |
square pyramid square antiprism |
pentagonal pyramid pentagonal antiprism |
Elongated cupolæ and rotundæ
| Elongated cupola | Elongated rotunda | Gyroelongated cupola | Gyroelongated rotunda | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coplanar | J18 | J19 | J20 | J21 | Concave | J22 | J23 | J24 | J25 |
| Elongated digonal cupola | Elongated triangular cupola | Elongated square cupola | Elongated pentagonal cupola | Elongated pentagonal rotunda | Gyroelongated digonal cupola | Gyroelongated triangular cupola | Gyroelongated square cupola | Gyroelongated pentagonal cupola | Gyroelongated pentagonal rotunda |
 |
 |
 |
 |
 |
 |
 |
 |
 |
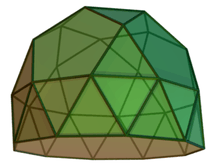 |
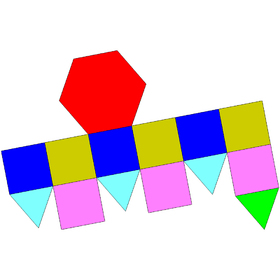 |
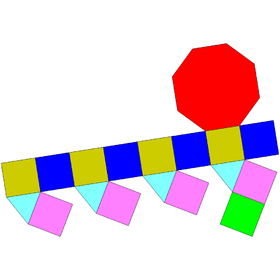 |
 |
 |
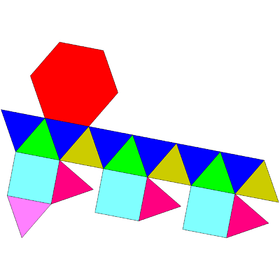 |
 |
 |
 | ||
| Augmented from polyhedra | |||||||||
| Square prism Triangular prism |
Hexagonal prism Triangular cupola |
Octagonal prism Square cupola |
Decagonal prism Pentagonal cupola |
Decagonal prism Pentagonal rotunda |
square antiprism Triangular prism |
Hexagonal antiprism Triangular cupola |
Octagonal antiprism Square cupola |
Decagonal antiprism Pentagonal cupola |
Decagonal antiprism Pentagonal rotunda |
Bicupolæ
The triangular gyrobicupola is a semiregular polyhedron (in this case an Archimedean solid), so it is not a Johnson solid.
| Orthobicupola | Gyrobicupola | ||||||
|---|---|---|---|---|---|---|---|
| Coplanar | J27 | J28 | J30 | J26 | Semiregular | J29 | J31 |
| Digonal orthobicupola | Triangular orthobicupola | Square orthobicupola | Pentagonal orthobicupola | Digonal gyrobicupola gyrobifastigium |
Triangular gyrobicupola (cuboctahedron) |
Square gyrobicupola | Pentagonal gyrobicupola |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Augmented from polyhedron | |||||||
| |
|
|
|
|
|
|
|
Cupola-rotundæ and birotunda
| Cupola-rotunda | Birotunda | ||
|---|---|---|---|
| J32 | J33 | J34 | Semiregular |
| Pentagonal orthocupolarotunda | Pentagonal gyrocupolarotunda | Pentagonal orthobirotunda | Pentagonal gyrobirotunda icosidodecahedron |
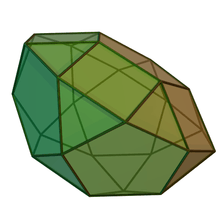 |
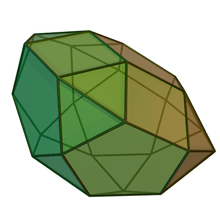 |
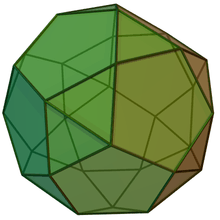 |
 |
 |
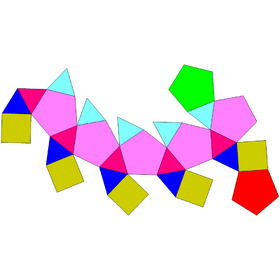 |
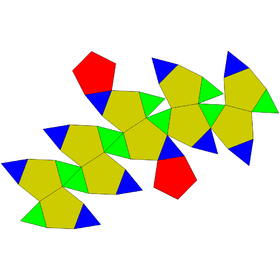 |
 |
| Augumented from polyhedra | |||
| Pentagonal cupola Pentagonal rotunda |
Pentagonal rotunda | ||
Elongated bicupolæ
| Elongated orthobicupola | Elongated gyrobicupola | ||||||
|---|---|---|---|---|---|---|---|
| Coplanar | J35 | Semiregular | J38 | Coplanar | J36 | J37 | J39 |
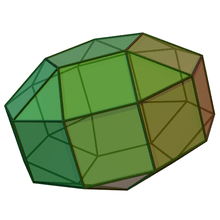
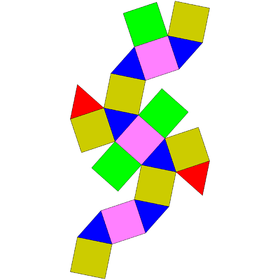
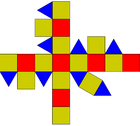
| Elongated digonal orthobicupola | Elongated triangular orthobicupola | Elongated square orthobicupola (rhombicuboctahedron) |
Elongated pentagonal orthobicupola | Elongated digonal gyrobicupola | Elongated triangular gyrobicupola | Elongated square gyrobicupola | Elongated pentagonal gyrobicupola |
 |
 |
 |
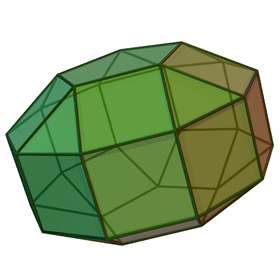 |
 |
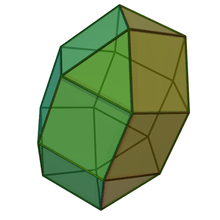 |
 |
 |
 |
 |
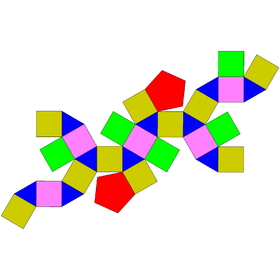 |
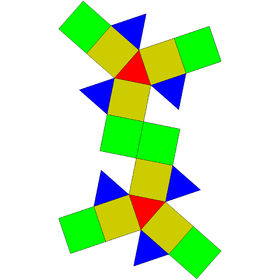 |
 |
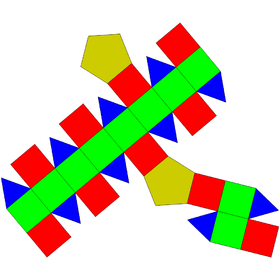 | ||
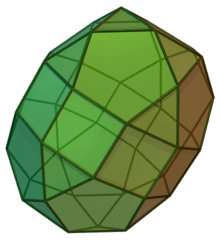
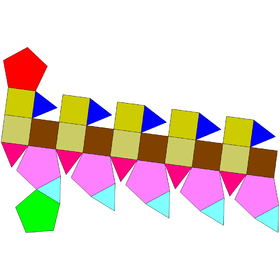
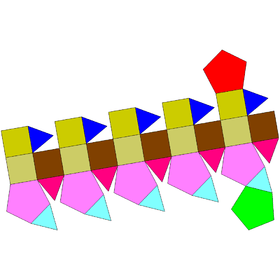
Elongated cupola-rotundæ and birotundæ
| Elongated cupolarotunda | Elongated birotunda | ||
|---|---|---|---|
| J40 | J41 | J42 | J43 |
| Elongated pentagonal orthocupolarotunda | Elongated pentagonal gyrocupolarotunda | Elongated pentagonal orthobirotunda | Elongated pentagonal gyrobirotunda |
 |
 |
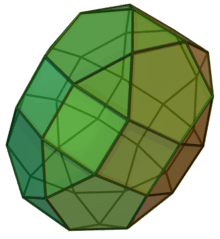 |
 |
 |
 |
 |
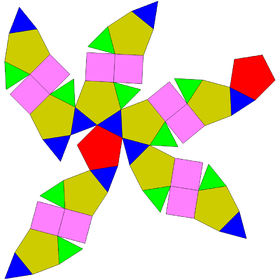 |
Gyroelongated bicupolæ, cupola-rotunda, and birotunda
These Johnson solids have 2 chiral forms.
| Gyroelongated bicupola | Gyroelongated cupolarotunda | Gyroelongated birotunda | |||
|---|---|---|---|---|---|
| Concave | J44 | J45 | J46 | J47 | J48 |
| Gyroelongated digonal bicupola | Gyroelongated triangular bicupola | Gyroelongated square bicupola | Gyroelongated pentagonal bicupola | Gyroelongated pentagonal cupolarotunda | Gyroelongated pentagonal birotunda |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Augmented from polyhedra | |||||
| Triangular prism Square antiprism |
Triangular cupola Hexagonal antiprism |
Square cupola Octagonal antiprism |
Pentagonal cupola Decagonal antiprism |
Pentagonal cupola Pentagonal rotunda Decagonal antiprism |
Pentagonal rotunda Decagonal antiprism |
| |
|
|
|
|
|
Augmented triangular prisms
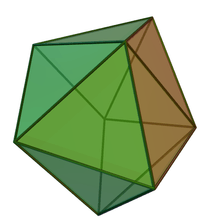
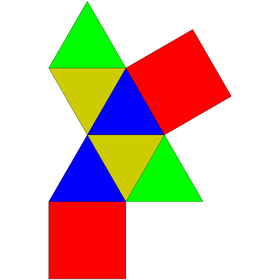
| J7 (repeat) |
J49 | J50 | J51 | |
|---|---|---|---|---|
| Elongated triangular pyramid | Augmented triangular prism | Biaugmented triangular prism | Triaugmented triangular prism | |
 |
 |
 |
 | |
 |
 |
 |
 | |
| Augumented from polyhedra | ||||
| Triangular prism tetrahedron |
Triangular prism Square pyramid | |||
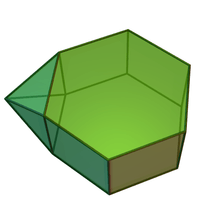
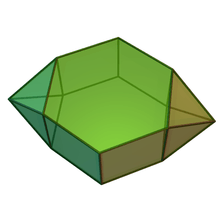
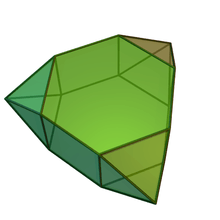
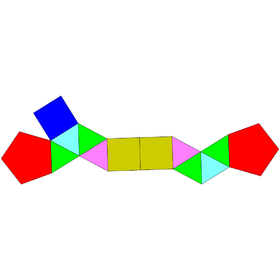
Augmented pentagonal and hexagonal prisms
| Augmented pentagonal prisms | Augmented hexagonal prisms | ||||
|---|---|---|---|---|---|
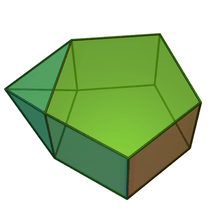
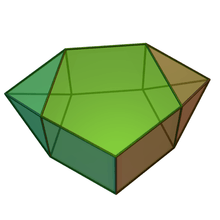
| J52 | J53 | J54 | J55 | J56 | J57 |
| Augmented pentagonal prism | Biaugmented pentagonal prism | Augmented hexagonal prism | Parabiaugmented hexagonal prism | Metabiaugmented hexagonal prism | Triaugmented hexagonal prism |
 |
 |
 |
 |
 |
 |
 |
 |
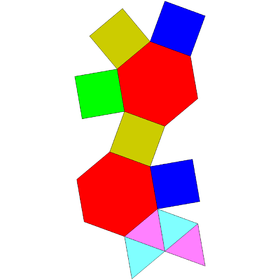 |
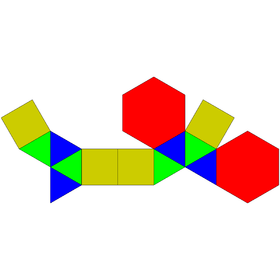 |
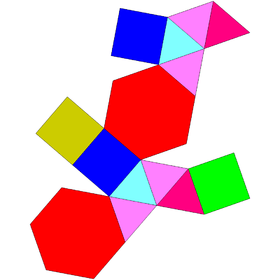 |
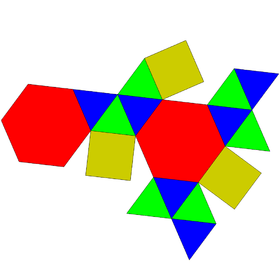 |
| Augumented from polyhedra | |||||
| Pentagonal prism Square pyramid |
Hexagonal prism Square pyramid | ||||
Augmented dodecahedra
| Regular | J58 | J59 | J60 | J61 |
|---|---|---|---|---|
| Dodecahedron | Augmented dodecahedron | Parabiaugmented dodecahedron | Metabiaugmented dodecahedron | Triaugmented dodecahedron |
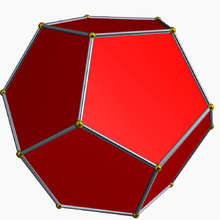 |
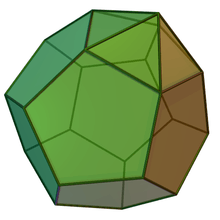 |
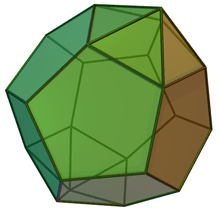 |
 |
 |
| |
 |
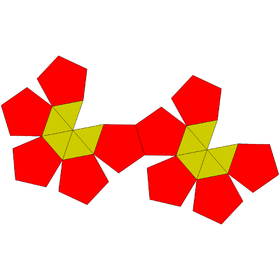 |
 |
 |
| Augumented from polyhedra | ||||
| Dodecahedron and pentagonal pyramid | ||||
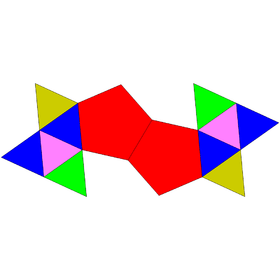
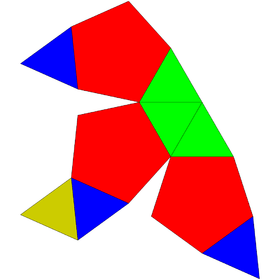
Diminished icosahedra
| J63 | J62 | J11 (Repeated) |
Regular | J64 |
|---|---|---|---|---|
| Tridiminished icosahedron | Metabidiminished icosahedron | Diminished icosahedron (Gyroelongated pentagonal pyramid) |
Icosahedron | Augmented tridiminished icosahedron |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
| Augumented from polyhedra | ||||
| Tridiminished icosahedron, pentagonal pyramid and tetrahedron | ||||
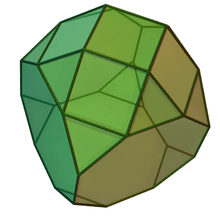
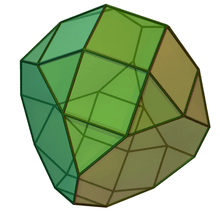
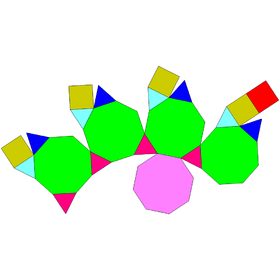
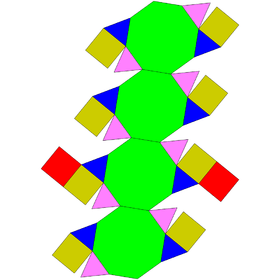
Augmented truncated tetrahedron and truncated cubes
| J65 | J66 | J67 |
|---|---|---|
| Augmented truncated tetrahedron | Augmented truncated cube | Biaugmented truncated cube |
 |
 |
 |
 |
 |
 |
| Augumented from polyhedra | ||
| truncated tetrahedron triangular cupola |
truncated cube square cupola | |
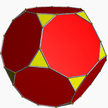
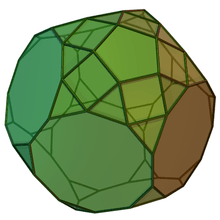
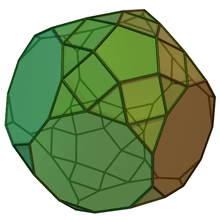
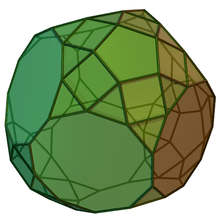
Augmented truncated dodecahedra
| Semiregular | J68 | J69 | J70 | J71 |
|---|---|---|---|---|
| Truncated dodecahedron | Augmented truncated dodecahedron | Parabiaugmented truncated dodecahedron | Metabiaugmented truncated dodecahedron | Triaugmented truncated dodecahedron |
 |
 |
 |
 |
 |
 |
 |
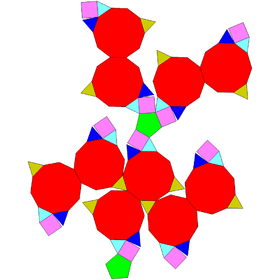 |
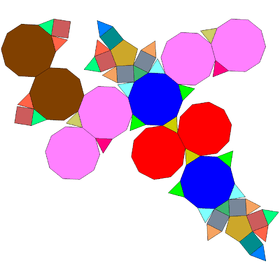 |
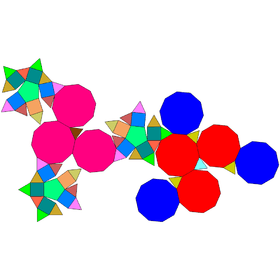 |
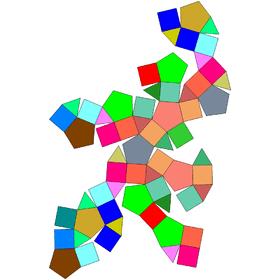
Gyrate rhombicosidodecahedra
| J72 | J73 | J74 | J75 |
|---|---|---|---|
| Gyrate rhombicosidodecahedron | Parabigyrate rhombicosidodecahedron | Metabigyrate rhombicosidodecahedron | Trigyrate rhombicosidodecahedron |
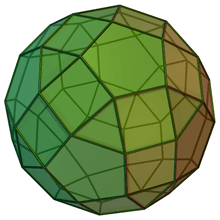 |
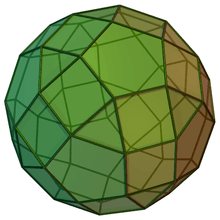 |
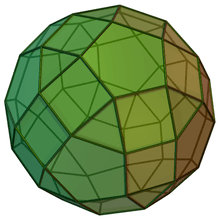 |
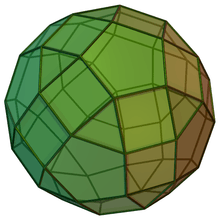 |
 |
 |
 |
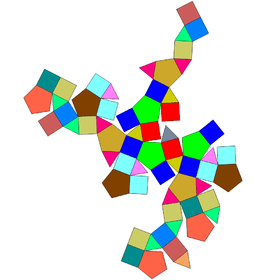 |
Diminished rhombicosidodecahedra
Snub antiprisms
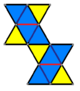
The snub antiprisms can be constructed as an alternation of a truncated antiprism. Two are Johnson solids, one is a regular, and the rest can not be constructed with regular triangles.
| J84 | Regular | J85 | Irregular |
|---|---|---|---|
| Johnson solid | Regular | Johnson solid | Concave... |
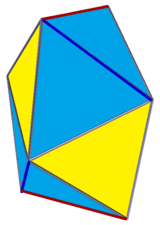 Snub disphenoid ss{2,4} |
 icosahedron ss{2,6} |
 snub square antiprism ss{2,8} |
ss{2,10}... |
 |
 |
 |
Others
| J86 | J87 | J88 | |
|---|---|---|---|
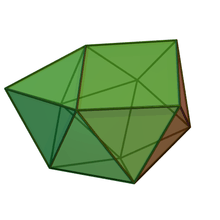
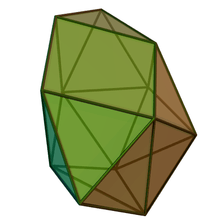
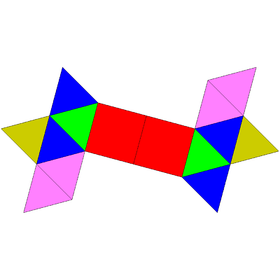
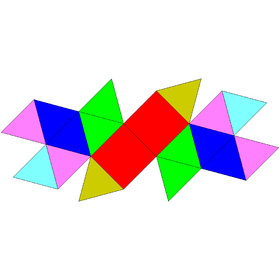
| Sphenocorona | Augmented sphenocorona | Sphenomegacorona | |
 |
 |
 | |
 |
 |
 | |
| J89 | J90 | J91 | J92 |
| Hebesphenomegacorona | Disphenocingulum | Bilunabirotunda | Triangular hebesphenorotunda |
 |
 |
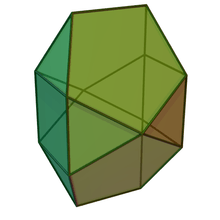 |
 |
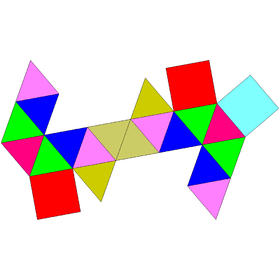 |
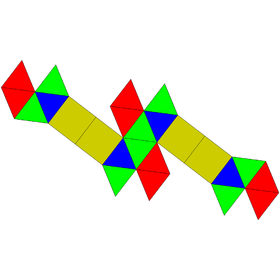 |
 |
 |
Classification by types of faces
Triangle-faced Johnson solids
Five Johnson solids are deltahedra, with all equilateral triangle faces:
Triangle and square-faced Johnson solids
Twenty four Johnson solids have only triangle or square faces:
Triangle and pentagonal-faced Johnson solids
Eleven Johnson solids have only triangle and pentagonal faces:
Triangle, square and hexagonal-faced Johnson solids
Eight Johnson solids have only triangle, square and hexagonal faces:
Triangle, square and octagonal-faced Johnson solids
Five Johnson solids have only triangle, square and octagonal faces:
Circumscribable Johnson solids
25 of the Johnson solids have vertices that exist on the surface of a sphere: 1-6,11,19,27,34,37,62,63,72-83. All of them can be seen to be related to a regular or uniform polyhedron by gyration, diminishment, or dissection.[3]
| Octahedron | Cuboctahedron | Rhombicuboctahedron | |||
|---|---|---|---|---|---|
| J1 |
J3 |
J27 |
J4 |
J19 |
J37 |
| Icosahedron | Icosidodecahedron | ||||
|---|---|---|---|---|---|
| J2 |
J63 |
J62 |
J11 |
J6 |
J34 |
J5 |
J76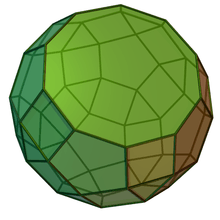 |
J80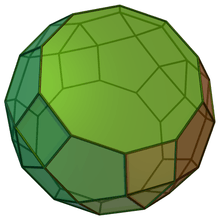 |
J81 |
J83 |
J72 |
J73 |
J74 |
J75 |
J77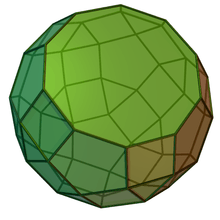 |
J78 |
J79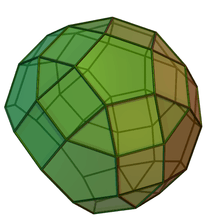 |
J82 |
See also
References
- Johnson, Norman W. (1966). "Convex Solids with Regular Faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Zalgaller, Victor A. (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. Zbl 0177.24802. No ISBN. The first proof that there are only 92 Johnson solids: see also Zalgaller, Victor A. (1967). "Convex Polyhedra with Regular Faces". Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova (in Russian). 2: 1–221. ISSN 0373-2703. Zbl 0165.56302.
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 3 Further Convex polyhedra
- ↑ http://www.georgehart.com/virtual-polyhedra/pseudo-rhombicuboctahedra.html
- ↑ George Hart (quoting Johnson) (1996). "Johnson Solids". Virtual Polyhedra. Retrieved 5 February 2014.
- ↑ http://bendwavy.org/klitzing/explain/johnson.htm
External links
- Sylvain Gagnon, "Convex polyhedra with regular faces", Structural Topology, No. 6, 1982, 83-95.
- Paper Models of Polyhedra Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W. "Johnson Solid". MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
- CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4-dimensional space