Prismatoid

In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes. Its lateral faces can be trapezoids or triangles.^[1] If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid.

Area

If the areas of the two parallel faces are A₁ and A₃, the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is A₂, and the height (the distance between the two parallel faces) is h, then the volume of the prismatoid is given by ${\displaystyle V={\frac {h(A_{1}+4A_{2}+A_{3})}{6}}}$ or ${\displaystyle V={\frac {nh(a^{2}+4b^{2}+c^{2})}{24\tan(180/n)}}}$(This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height.)

Prismatoid families

Pyramids	Wedges	Parallelepipeds	Prisms	Antiprisms			Cupolae	Frusta

Families of prismatoids include:

• Pyramids, where one plane contains only a single point;
• Wedges, where one plane contains only two points;
• Prisms, where the polygons in each plane are congruent and joined by rectangles or parallelograms;
• Antiprisms, where the polygons in each plane are congruent and joined by an alternating strip of triangles;
• Crossed antiprisms;
• Cupolae, where the polygon in one plane contains twice as many points as the other and is joined to it by alternating triangles and rectangles;
• Frusta obtained by truncation of a pyramid;
• Quadrilateral-faced hexahedral prismatoids:
  1. Parallelepipeds - six parallelogram faces
  2. Rhombohedrons - six rhombus faces
  3. Trigonal trapezohedra - six congruent rhombus faces
  4. Cuboids - six rectangular faces
  5. Quadrilateral frusta - an apex-truncated square pyramid
  6. Cube - six square faces

Higher dimensions

In general a polytope is prismatoidal if its vertices exist in two hyperplanes. For example in 4-dimensions, two polyhedra can be placed in 2 parallel 3-spaces, and connected with polyhedral sides.

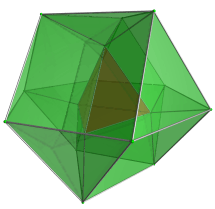
A tetrahedral-cuboctahedral cupola.

References

1. William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.75

External links

• Weisstein, Eric W. "Prismatoid". MathWorld.