Parabolic coordinates

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.
Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect and the potential theory of the edges.
Two-dimensional parabolic coordinates
Two-dimensional parabolic coordinates are defined by the equations, in terms of cartesian coordinates:
The curves of constant form confocal parabolae
that open upwards (i.e., towards ), whereas the curves of constant form confocal parabolae
that open downwards (i.e., towards ). The foci of all these parabolae are located at the origin.
Two-dimensional scale factors
The scale factors for the parabolic coordinates are equal
Hence, the infinitesimal element of area is
and the Laplacian equals
Other differential operators such as and can be expressed in the coordinates by substituting the scale factors into the general formulae found in orthogonal coordinates.
Three-dimensional parabolic coordinates
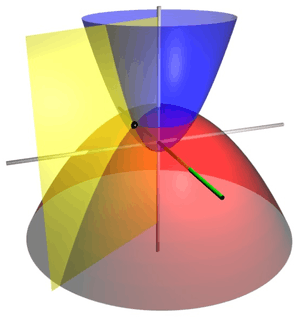
The two-dimensional parabolic coordinates form the basis for two sets of three-dimensional orthogonal coordinates. The parabolic cylindrical coordinates are produced by projecting in the -direction. Rotation about the symmetry axis of the parabolae produces a set of confocal paraboloids, the coordinate system of tridimensional parabolic coordinates. Expressed in terms of cartesian coordinates:
where the parabolae are now aligned with the -axis, about which the rotation was carried out. Hence, the azimuthal angle is defined
The surfaces of constant form confocal paraboloids
that open upwards (i.e., towards ) whereas the surfaces of constant form confocal paraboloids
that open downwards (i.e., towards ). The foci of all these paraboloids are located at the origin.
The Riemannian metric tensor associated with this coordinate system is
Three-dimensional scale factors
The three dimensional scale factors are:
It is seen that The scale factors and are the same as in the two-dimensional case. The infinitesimal volume element is then
and the Laplacian is given by
Other differential operators such as and can be expressed in the coordinates by substituting the scale factors into the general formulae found in orthogonal coordinates.
See also
Bibliography
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 660. ISBN 0-07-043316-X. LCCN 52011515.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 185–186. LCCN 55010911.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 180. LCCN 59014456. ASIN B0000CKZX7.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 96. LCCN 67025285.
- Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), substituting uk for ξk.
- Moon P, Spencer DE (1988). "Parabolic Coordinates (μ, ν, ψ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 34–36 (Table 1.08). ISBN 978-0-387-18430-2.
External links
- Hazewinkel, Michiel, ed. (2001), "Parabolic coordinates", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- MathWorld description of parabolic coordinates