Truncated trapezohedron
| Set of truncated trapezohedra | |
|---|---|
 | |
| Faces | 2 n-gons, 2n pentagons |
| Edges | 6n |
| Vertices | 4n |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | gyroelongated dipyramids |
| Properties | convex |
An n-gonal truncated trapezohedron is a polyhedron formed by a n-gonal trapezohedron with n-gonal pyramids truncated from its two polar axis vertices. If the polar vertices are completely truncated (diminished), a trapezohedron becomes an antiprism.
The vertices exist as 4 n-gons in four parallel planes, with alternating orientation in the middle creating the pentagons.
The regular dodecahedron is the most common polyhedron in this class, being a platonic solid, with 12 congruent pentagonal faces.
A truncated trapezohedron has all vertices with 3 faces. This means that the dual polyhedra, the set of gyroelongated dipyramids, have all triangular faces. For example, the icosahedron is the dual of the dodecahedron.
Forms
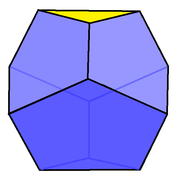
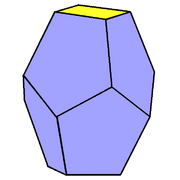

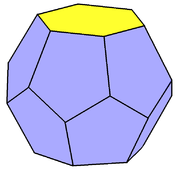
- Triangular truncated trapezohedron (Dürer's solid) – 6 pentagons, 2 triangles, dual gyroelongated triangular dipyramid
- Truncated square trapezohedron – 8 pentagons, 2 squares, dual gyroelongated square dipyramid
- Truncated pentagonal trapezohedron or regular dodecahedron – 12 pentagonal faces, dual icosahedron
- Truncated hexagonal trapezohedron – 12 pentagons, 2 hexagons, dual gyroelongated hexagonal dipyramid
- ...
- Truncated n-gonal trapezohedron – 2n pentagons, 2 n-gons, dual gyroelongated dipyramids
See also
External links
- Conway Notation for Polyhedra Try: "tndAn", where n=4,5,6... example "t5dA5" is a dodecahedron.
This article is issued from Wikipedia - version of the 11/7/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.