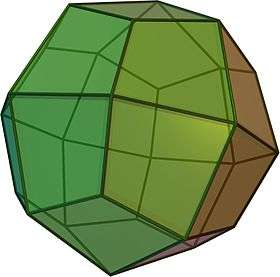
Deltoidal icositetrahedron

Deltoidal icositetrahedron
Animated
Type	Catalan
Conway notation	oC or deC
Coxeter diagram
Face polygon	kite
Faces	24
Edges	48
Vertices	26 = 6 + 8 + 12
Face configuration	V3.4.4.4
Symmetry group	Oh, BC3, [4,3], *432
Rotation group	O, [4,3]^+, (432)
Dihedral angle	138°07′05″ arccos(−7 + 4√2/17)
Dual polyhedron	rhombicuboctahedron
Properties	convex, face-transitive
Net

In geometry, a deltoidal icositetrahedron (also a trapezoidal icositetrahedron, tetragonal icosikaitetrahedron,^[1] and strombic icositetrahedron) is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron.

Dimensions

The 24 faces are kites. The short and long edges of each kite are in the ratio 1:(2 − 1/√2) ≈ 1:1.292893...

If its smallest edges have length 1, its surface area is $\scriptstyle{6\sqrt{29-2\sqrt{2}}}$ and its volume is $\scriptstyle{\sqrt{122+71\sqrt{2}}}$.

Occurrences in nature and culture

The deltoidal icositetrahedron is a crystal habit often formed by the mineral analcime and occasionally garnet. The shape is often called a trapezohedron in mineral contexts, although in solid geometry that name has another meaning.

Orthogonal projections

The deltoidal icositetrahedron has three symmetry positions, all centered on vertices:

Orthogonal projections

Projective symmetry	[2]	[4]	[6]
Image
Dual image

Related polyhedra

The great triakis octahedron is a stellation of the deltoidal icositetrahedron.

Dyakis dodecahedron

The deltoidal icositetrahedron is topologically equivalent to a cube whose faces are divided in quadrants. It can also be projected onto a regular octahedron, with kite faces, or more general quadrilaterals with pyritohedral symmetry. In Conway polyhedron notation, they represent an ortho operation to a cube or octahedron.

In crystallography a rotational variation is called a dyakis dodecahedron^[2][3] or diploid.^[4]

Octahedral, Oh, order 24		Pyritohedral, Th, order 12

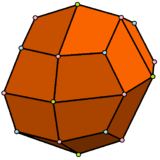Related polyhedra and tilings

Spherical deltoidal icositetrahedron

The deltoidal icositetrahedron is one of a family of duals to the uniform polyhedra related to the cube and regular octahedron.

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)							[4,3]^+ (432)	[1^+,4,3] = [3,3] (*332)		[3^+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{3^1,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V4^3	V3.8^2	V(3.4)^2	V4.6^2	V3^4	V3.4^3	V4.6.8	V3^4.4	V3^3	V3.6^2	V3^5

This polyhedron is topologically related as a part of sequence of deltoidal polyhedra with face figure (V3.4.n.4), and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.

*n42 symmetry mutation of dual expanded tilings: V3.4.n.4

Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure Config.	V3.4.2.4	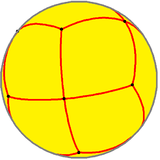V3.4.3.4	V3.4.4.4	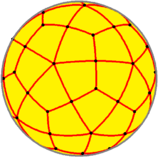V3.4.5.4	V3.4.6.4	V3.4.7.4	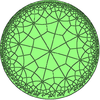V3.4.8.4	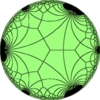V3.4.∞.4

See also

• Deltoidal hexecontahedron
• Tetrakis hexahedron, another 24-face Catalan solid which looks a bit like an overinflated cube.
• "The Haunter of the Dark", a story by H.P. Lovecraft, whose plot involves this figure

References

1. Conway, Symmetries of Things, p.284–286
2. Isohedron 24k
3. The Isometric Crystal System
4. https://www.uwgb.edu/dutchs/symmetry/xlforms.htm

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 23, Deltoidal icositetrahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal icosikaitetrahedron)

External links

• Eric W. Weisstein, Deltoidal icositetrahedron (Catalan solid) at MathWorld.
• Deltoidal (Trapezoidal) Icositetrahedron – Interactive Polyhedron model