Triakis icosahedron
| Triakis icosahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kI |
| Face type | V3.10.10 isosceles triangle |
| Faces | 60 |
| Edges | 90 |
| Vertices | 32 |
| Vertices by type | 20{3}+12{10} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 160°36′45″ arccos(−24 + 15√5/61) |
| Properties | convex, face-transitive |
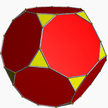 Truncated dodecahedron (dual polyhedron) |
 Net |
In geometry, the triakis icosahedron (or kisicosahedron[1]) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.
Orthogonal projections
The triakis icosahedron has three symmetry positions, two on vertices, and one on a midedge: The Triakis icosahedron has five special orthogonal projections, centered on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A2 and H2 Coxeter planes.
| Projective symmetry |
[2] | [6] | [10] |
|---|---|---|---|
| Image |  |
 |
 |
| Dual image |
 |
 |
 |
Kleetope
It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron. This interpretation is expressed in the name, triakis.
Other triakis icosahedra
This interpretation can also apply to other similar nonconvex polyhedra with pyramids of different heights:
 First stellation of icosahedron, or small triambic icosahedron (sometimes called a triakis icosahedron)
First stellation of icosahedron, or small triambic icosahedron (sometimes called a triakis icosahedron)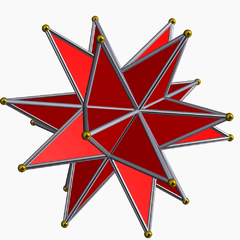 Great stellated dodecahedron (with very tall pyramids)
Great stellated dodecahedron (with very tall pyramids)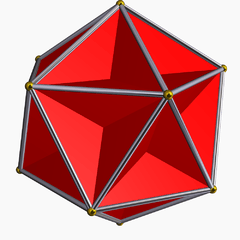 Great dodecahedron (with inverted pyramids)
Great dodecahedron (with inverted pyramids)
Stellations

The triakis icosahedron has numerous stellations, including this one.
Related polyhedra
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 |
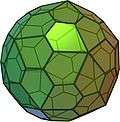 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
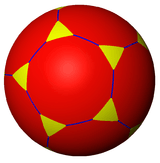
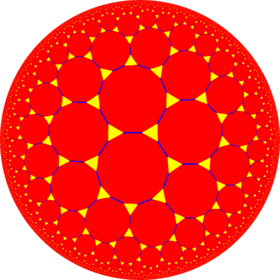
The triakis icosahedron is a part of a sequence of polyhedra and tilings, extending into the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of truncated tilings: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Truncated figures |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | t{12i,3} | t{9i,3} | t{6i,3} |
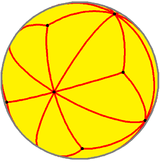
| Triakis figures |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
See also
- Triakis triangular tiling for other "triakis" polyhedral forms.
- Great triakis icosahedron
References
- ↑ Conway, Symmetries of things, p.284
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 730208. (The thirteen semiregular convex polyhedra and their duals, Page 19, Triakisicosahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis icosahedron )
External links
- Eric W. Weisstein, Triakis icosahedron (Catalan solid) at MathWorld.
- Triakis Icosahedron – Interactive Polyhedron Model
