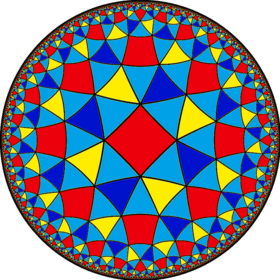
Alternated octagonal tiling
| Tritetragonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (3.4)3 |
| Schläfli symbol | (4,3,3) s(4,4,4) |
| Wythoff symbol | 3 | 3 4 |
| Coxeter diagram | |
| Symmetry group | [(4,3,3)], (*433) [(4,4,4)]+, (444) |
| Dual | Order-4-3-3_t0 dual tiling |
| Properties | Vertex-transitive |
In geometry, the tritetragonal tiling or alternated octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbols of {(4,3,3)} or h{8,3}.
Geometry
Although a sequence of edges seem to represent straight lines (projected into curves), careful attention will show they are not straight, as can be seen by looking at it from different projective centers.
 Triangle-centered hyperbolic straight edges |
 Edge-centered projective straight edges |
 Point-centered projective straight edges |
Dual tiling

In art
Circle Limit III is a woodcut made in 1959 by Dutch artist M. C. Escher, in which "strings of fish shoot up like rockets from infinitely far away" and then "fall back again whence they came". White curves within the figure, through the middle of each line of fish, divide the plane into squares and triangles in the pattern of the tritetragonal tiling. However, in the tritetragonal tiling, the corresponding curves are chains of hyperbolic line segments, with a slight angle at each vertex, while in Escher's woodcut they appear to be smooth hypercycles.
Related polyhedra and tiling
| Uniform (4,3,3) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| h{8,3} t0(4,3,3) |
r{3,8}1/2 t0,1(4,3,3) |
h{8,3} t1(4,3,3) |
h2{8,3} t1,2(4,3,3) |
{3,8}1/2 t2(4,3,3) |
h2{8,3} t0,2(4,3,3) |
t{3,8}1/2 t0,1,2(4,3,3) |
s{3,8}1/2 s(4,3,3) | ||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V(3.4)3 | V3.8.3.8 | V(3.4)3 | V3.6.4.6 | V(3.3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | ||||
| Uniform (4,4,4) tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,4)], (*444) | [(4,4,4)]+ (444) |
[(1+,4,4,4)] (*4242) |
[(4+,4,4)] (4*22) | ||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| t0(4,4,4) h{8,4} |
t0,1(4,4,4) h2{8,4} |
t1(4,4,4) {4,8}1/2 |
t1,2(4,4,4) h2{8,4} |
t2(4,4,4) h{8,4} |
t0,2(4,4,4) r{4,8}1/2 |
t0,1,2(4,4,4) t{4,8}1/2 |
s(4,4,4) s{4,8}1/2 |
h(4,4,4) h{4,8}1/2 |
hr(4,4,4) hr{4,8}1/2 | ||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V(4.4)4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V88 | V(4,4)3 | ||
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
| Wikimedia Commons has media related to Uniform tiling 3-4-3-4-3-4. |
- Douglas Dunham Department of Computer Science University of Minnesota, Duluth
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch

