Uniform coloring
 111 |
 112 |
 123 |
|---|---|---|
| The hexagonal tiling has 3 uniform colorings. | ||
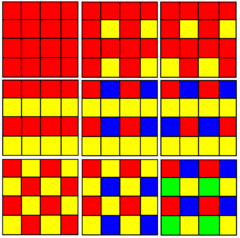
1111, 1112(a), 1112(b),
1122, 1123(a), 1123(b),
1212, 1213, 1234.
In geometry, a uniform coloring is a property of a uniform figure (uniform tiling or uniform polyhedron) that is colored to be vertex-transitive. Different symmetries can be expressed on the same geometric figure with the faces following different uniform color patterns.
A uniform coloring can be specified by listing the different colors with indices around a vertex figure.
n-uniform figures
In addition, an n-uniform coloring is a property of a uniform figure which has n types vertex figure, that are collectively vertex transitive.
Archimedean coloring
A related term is Archimedean color requires one vertex figure coloring repeated in a periodic arrangement. A more general term are k-Archimedean colorings which count k distinctly colored vertex figures.
For example this Archimedean coloring (left) of a triangular tiling has two colors, but requires 4 unique colors by symmetry positions and become a 2-uniform coloring (right):
 1-Archmedean coloring 111112 |
 2-uniform coloring 112344 and 121434 |
References
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. Uniform and Archimedean colorings, pp. 102–107
External links
- Uniform Tessellations on the Euclid plane
- Tessellations of the Plane
- David Bailey's World of Tessellations
- k-uniform tilings
- n-uniform tilings
