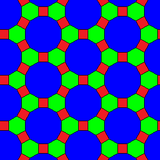
Rhombitrihexagonal tiling
| Rhombitrihexagonal tiling | |
|---|---|
 | |
| Type | Semiregular tiling |
| Vertex configuration |  3.4.6.4 |
| Schläfli symbol | rr{6,3} or |
| Wythoff symbol | 3 | 6 2 |
| Coxeter diagram | |
| Symmetry | p6m, [6,3], (*632) |
| Rotation symmetry | p6, [6,3]+, (632) |
| Bowers acronym | Rothat |
| Dual | Deltoidal trihexagonal tiling |
| Properties | Vertex-transitive |
In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.
John Conway calls it a rhombihexadeltille.[1] It can be considered a cantellated by Norman Johnson's terminology or an expanded hexagonal tiling by Alicia Boole Stott's operational language.
There are 3 regular and 8 semiregular tilings in the plane.
Uniform colorings
There is only one uniform coloring in a rhombitrihexagonal tiling. (Naming the colors by indices around a vertex (3.4.6.4): 1232.)
With edge-colorings there is a half symmetry form (3*3) orbifold notation. The hexagons can be considered as truncated triangles, t{3} with two types of edges. It has Coxeter diagram ![]()
![]()
![]()
![]()
![]() , Schläfli symbol s2{3,6}. The bicolored square can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, a triangular tiling results, constructed as a snub triangular tiling,
, Schläfli symbol s2{3,6}. The bicolored square can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, a triangular tiling results, constructed as a snub triangular tiling, ![]()
![]()
![]()
![]()
![]() .
.
| Symmetry | [6,3], (*632) | [6,3+], (3*3) | ||
|---|---|---|---|---|
| Name | Rhombitrihexagonal | Cantic snub triangular | Snub triangular | |
| Image |  Uniform face coloring |
 Uniform edge coloring |
 Nonuniform geometry |
 Limit |
| Schläfli symbol |
rr{3,6} | s2{3,6} | s{3,6} | |
| Coxeter diagram |
||||
Examples
 An ornamental version |
 Nonuniform pattern (with rectangles) |
 The game Kensington |
Church floor tiling, Sevilla, Spain |
 The tiling can be replaced by circular edges, centered on the hexagons. In quilting it is call Jacks chain.[2] |
Related polyhedra and tilings
There is one related 2-uniform tilings, having hexagons dissected into 6 triangles.[3][4]
 3.4.6.4 |
  |
 3.3.4.3.4 & 36 |
|---|
The rhombitrihexagonal tiling is related to the truncated trihexagonal tiling by replacing some of the hexagons and surrounding squares and triangles with dodecagons:
 3.4.6.4 |
  |
 4.6.12 |
Circle packing
The rhombitrihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 4 other circles in the packing (kissing number).[5] The translational lattice domain (red rhombus) contains 6 distinct circles. The gap inside each hexagon allows for one circle, related to a 2-uniform tiling with the hexagons divided into 6 triangles.


Wythoff construction
There are eight uniform tilings that can be based from the regular hexagonal tiling (or the dual triangular tiling).
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)
| Uniform hexagonal/triangular tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,3], (*632) | [6,3]+ (632) |
[6,3+] (3*3) | |||||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | s{3,6} | |||
 |
 |
 |
 |
 |
 |
 |
 |
 | |||
| 63 | 3.122 | (3.6)2 | 6.6.6 | 36 | 3.4.12.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | |||
| V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.12.4 | V.4.6.12 | V34.6 | V36 | |||
Symmetry mutations
This tiling is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of expanded tilings: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paracomp. | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure |  |
 |
 |
 |
 |
 |
 | |
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Deltoidal trihexagonal tiling
| Deltoidal trihexagonal tiling | |
|---|---|
 | |
| Type | Dual semiregular tiling |
| Coxeter diagram | |
| Faces | kite |
| Face configuration | V3.4.6.4 |
| Symmetry group | p6m, [6,3], (*632) |
| Rotation group | p6, [6,3]+, (632) |
| Dual | Rhombitrihexagonal tiling |
| Properties | face-transitive |
The deltoidal trihexagonal tiling is a dual of the semiregular tiling known as the rhombitrihexagonal tiling. Conway calls it a tetrille.[1] The edges of this tiling can be formed by the intersection overlay of the regular triangular tiling and a hexagonal tiling. Each kite face of this tiling has angles 120°, 90°, 60° and 90°. It is one of only eight tilings of the plane in which every edge lies on a line of symmetry of the tiling.[6]
The deltoidal trihexagonal tiling is a dual of the semiregular tiling rhombitrihexagonal tiling.[7] Its faces are deltoids or kites.
Related polyhedra and tilings
It is one of 7 dual uniform tilings in hexagonal symmetry, including the regular duals.
| Symmetry: [6,3], (*632) | [6,3]+, (632) | |||||
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| V63 | V3.122 | V(3.6)2 | V36 | V3.4.12.4 | V.4.6.12 | V34.6 |
This tiling has face transitive variations, that can distort the kites into bilateral trapezoids or more general quadrillaterals. Ignoring the face colors below, the fully symmetry is p6m, and the lower symmetry is p31m with 3 mirrors meeting at a point, and 3-fold rotation points.[8]
| Symmetry | p6m, [6,3], (*632) | p31m, [6,3+], (3*3) | |
|---|---|---|---|
| Form |  |
 |
 |
| Faces | Kite | Half regular hexagon | Quadrilaterals |
This tiling is related to the trihexagonal tiling by dividing the triangles and hexagons into central triangles and merging neighboring triangles into kites.
The deltoidal trihexagonal tiling is a part of a set of uniform dual tilings, corresponding to the dual of the rhombitrihexagonal tiling.
Symmetry mutations
This tiling is topologically related as a part of sequence of tilings with face configurations V3.4.n.4, and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure Config. |
 V3.4.2.4 |
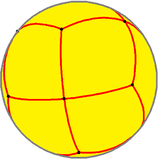 V3.4.3.4 |
 V3.4.4.4 |
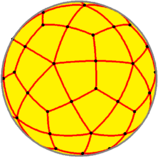 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
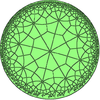 V3.4.8.4 |
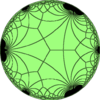 V3.4.∞.4 |
Other deltoidal (kite) tiling
Other deltoidal tilings are possible.
Point symmetry allows the plane to be filled by growing kites, with the topology as a square tiling, V4.4.4.4, and can be created by crossing string of a dream catcher. Below is an example with dihedral hexagonal symmetry.
Another face transitive tiling with kite faces, also a topological variation of a square tiling and with face configuration V4.4.4.4. It is also vertex transitive, with every vertex containing all orientations of the kite face.
| Symmetry | D6, [6], (*66) | pmg, [∞,(2,∞)+], (22*) | p6m, [6,3], (*632) |
|---|---|---|---|
| Tiling |  |
 |
 |
| Configuration | V4.4.4.4 | V6.4.3.4 | |
See also
| Wikimedia Commons has media related to Uniform tiling 3-4-6-4. |
Notes
- 1 2 Conway, 2008, p288 table
- ↑ Ring Cycles a Jacks Chain variation
- ↑ Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
- ↑ http://www.uwgb.edu/dutchs/symmetry/uniftil.htm
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, pattern B
- ↑ Kirby, Matthew; Umble, Ronald (2011), "Edge tessellations and stamp folding puzzles", Mathematics Magazine, 84 (4): 283–289, arXiv:0908.3257
 , doi:10.4169/math.mag.84.4.283, MR 2843659.
, doi:10.4169/math.mag.84.4.283, MR 2843659. - ↑ Weisstein, Eric W. "Dual tessellation". MathWorld. (See comparative overlay of this tiling and its dual)
- ↑ Tilings and Patterns
References
- Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p40
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings.
- Weisstein, Eric W. "Uniform tessellation". MathWorld.
- Klitzing, Richard. "2D Euclidean tilings x3o6x - rothat - O8".
- Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern N, Dual p. 77-76, pattern 2
- Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–56, dual p. 116


