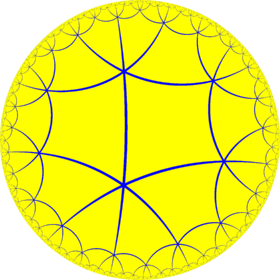
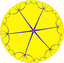
Order-4 hexagonal tiling
| Order-4 hexagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex figure | 64 |
| Schläfli symbol | {6,4} |
| Wythoff symbol | 4 | 6 2 |
| Coxeter diagram | |
| Symmetry group | [6,4], (*642) |
| Dual | Order-6 square tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the order-4 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,4}.
Symmetry
This tiling represents a hyperbolic kaleidoscope of 6 mirrors defining a regular hexagon fundamental domain. This symmetry by orbifold notation is called *222222 with 6 order-2 mirror intersections. In Coxeter notation can be represented as [6*,4], removing two of three mirrors (passing through the hexagon center). Adding a bisecting mirror through 2 vertices of a hexagonal fundamental domain defines a trapezohedral *3322 symmetry. Adding 3 bisecting mirrors through the vertices defines *443 symmetry. Adding 3 bisecting mirrors through the edge defines *3222 symmetry. Adding all 6 bisectors leads to full *642 symmetry.
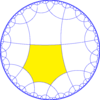 *222222 |
 *443 |
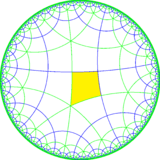 *3222 |
 *642 |
Uniform colorings
There are 7 distinct uniform colorings for the order-4 hexagonal tiling. They are similar to 7 of the uniform colorings of the square tiling, but exclude 2 cases with order-2 gyrational symmetry. Four of them have reflective constructions and Coxeter diagrams while three of them are undercolorings.
| 1 color | 2 colors | 3 and 2 colors | 4, 3 and 2 colors | ||||
|---|---|---|---|---|---|---|---|
| Uniform Coloring |
 (1111) |
 (1212) |
 (1213) |
 (1113) |
 (1234) |
 (1123) |
 (1122) |
| Symmetry | [6,4] (*642) |
[6,6] (*662) |
[(6,6,3)] = [6,6,1+] (*663) |
[1+,6,6,1+] (*3333) | |||
| Symbol | {6,4} | r{6,6} = {6,4}1/2 | r(6,3,6) = r{6,6}1/2 | r{6,6}1/4 | |||
| Coxeter diagram |
|||||||
Related polyhedra and tiling
This tiling is topologically related as a part of sequence of regular tilings with hexagonal faces, starting with the hexagonal tiling, with Schläfli symbol {6,n}, and Coxeter diagram ![]()
![]()
![]()
![]()
![]() , progressing to infinity.
, progressing to infinity.
| *n62 symmetry mutation of regular tilings: {6,n} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | ||||||
 {6,2} |
 {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
... |  {6,∞} |
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram ![]()
![]()
![]()
![]()
![]() , with n progressing to infinity.
, with n progressing to infinity.
| *n42 symmetry mutation of regular tilings: {n,4} | |||||||
|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | |||||
 |
 |
 |
 |
 |
 |
 | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
| Symmetry mutation of quasiregular tilings: 6.n.6.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *6n2 [n,6] |
Euclidean | Compact hyperbolic | Paracompact | Noncompact | |||||||
| *632 [3,6] |
*642 [4,6] |
*652 [5,6] |
*662 [6,6] |
*762 [7,6] |
*862 [8,6]... |
*∞62 [∞,6] |
[iπ/λ,6] | ||||
| Quasiregular figures configuration |
 6.3.6.3 |
 6.4.6.4 |
 6.5.6.5 |
 6.6.6.6 |
 6.7.6.7 |
 6.8.6.8 |
 6.∞.6.∞ |
6.∞.6.∞ | |||
| Dual figures | |||||||||||
| Rhombic figures configuration |
 V6.3.6.3 |
 V6.4.6.4 |
 V6.5.6.5 |
 V6.6.6.6 |
V6.7.6.7 |
 V6.8.6.8 |
 V6.∞.6.∞ |
||||
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
= = = |
= |
= = = |
= |
= = = |
= |
||||||
 |
 |
 |
 |
 |
 |
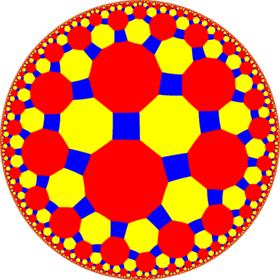 | |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 | |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
= |
= |
= |
= |
= |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
| Uniform hexahexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [6,6], (*662) | ||||||
= |
= |
= |
= |
= |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {6,6} = h{4,6} |
t{6,6} = h2{4,6} |
r{6,6} {6,4} |
t{6,6} = h2{4,6} |
{6,6} = h{4,6} |
rr{6,6} r{6,4} |
tr{6,6} t{6,4} |
| Uniform duals | ||||||
 |
 |
 |
 |
 |
 |
 |
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Alternations | ||||||
| [1+,6,6] (*663) |
[6+,6] (6*3) |
[6,1+,6] (*3232) |
[6,6+] (6*3) |
[6,6,1+] (*663) |
[(6,6,2+)] (2*33) |
[6,6]+ (662) |
 |
 |
 |
 |
 | ||
| h{6,6} | s{6,6} | hr{6,6} | s{6,6} | h{6,6} | hrr{6,6} | sr{6,6} |
| Similar H2 tilings in *3232 symmetry | ||||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter diagrams |
||||||||
| | | | |
| | |||
| Vertex figure |
66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Image |  |
 |
 |
 | ||||
| Dual |  |
 | ||||||
| Uniform tilings in symmetry *3222 | ||||
|---|---|---|---|---|
 |
.png) |
 |
 | |
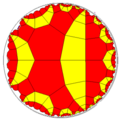 |
 |
.png) | ||
 |
 |
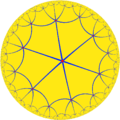 | ||
See also
| Wikimedia Commons has media related to Order-4 hexagonal tiling. |
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
