Hendecagram
| Regular hendecagrams | |
|---|---|
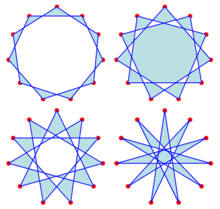 Four forms | |
| Edges and vertices | 11 |
| Schläfli symbol |
{11/2}, {11/3} {11/4}, {11/5} |
| Coxeter diagram |
|
| Symmetry group | Dih11, order 22 |
| Internal angle (degrees) |
≈114.545° {11/2} ≈81.8182° {11/3} ≈49.0909° {11/4} ≈16.3636° {11/5} |
In geometry, a hendecagram (also endecagram or endekagram) is a star polygon that has eleven vertices.
The name hendecagram combines a Greek numeral prefix, hendeca-, with the Greek suffix -gram. The hendeca- prefix derives from Greek ἕνδεκα (ἕν + δέκα, one + ten) meaning "eleven". The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[1]
Regular hendecagrams
There are four regular hendecagrams,[2] which can be described by the notation {11/2}, {11/3}, {11/4}, and {11/5}; in this notation, the number after the slash indicates the number of steps between pairs of points that are connected by edges. These same four forms can also be considered as stellations of a regular hendecagon.[3]
 {11/2} |
 {11/3} |
 {11/4} |
 {11/5} |
Construction
As with all odd regular polygons and star polygons whose orders are not products of distinct Fermat primes, the regular hendecagrams cannot be constructed with compass and straightedge.[4] However, Hilton & Pedersen (1986) describe folding patterns for making the hendecagrams {11/3}, {11/4}, and {11/5} out of strips of paper.[5]
Applications
.jpg)
Prisms over the hendecagrams {11/3} and {11/4} may be used to approximate the shape of DNA molecules.[6]
Fort Wood, now the base of the Statue of Liberty in New York City, is a star fort in the form of an irregular 11-point star.[7]
The Topkapı Scroll contains images of an 11-pointed star Girih form used in Islamic art. The star in this scroll is not one of the regular forms of the hendecagram, but instead uses lines that connect the vertices of a hendecagon to nearly-opposite midpoints of the hendecagon's edges.[8]
An 11-point star-shaped cross-section was used in the Space Shuttle Solid Rocket Booster, for the core of the forward section of the rocket (the hollow space within which the fuel burns). This design provided more surface area and greater thrust in the earlier part of a launch, and a slower burn rate and reduced thrust after the points of the star were burned away, at approximately the same time as the rocket passed the sound barrier.[9]
See also
References
- ↑ Liddell, Henry George; Scott, Robert (1940), A Greek-English Lexicon: γραμμή, Oxford: Clarendon Press
- ↑ O'Daffer, Phares G.; Clemens, Stanley R. (1976), Geometry: an investigative approach, Addison-Wesley, Exercise 7, p. 62, ISBN 9780201054200.
- ↑ Agricola, Ilka; Friedrich, Thomas (2008), Elementary Geometry, Student mathematical library, 43, American Mathematical Society, p. 96, ISBN 9780821890677.
- ↑ Carstensen, Celine; Fine, Benjamin; Rosenberger, Gerhard (2011), Abstract Algebra: Applications to Galois Theory, Algebraic Geometry, and Cryptography, Sigma series in pure mathematics, 11, Walter de Gruyter, p. 88, ISBN 9783110250084,
On the other hand a regular 11-gon is not constructible.
- ↑ Hilton, Peter; Pedersen, Jean (1986), "Symmetry in mathematics", Computers & Mathematics with Applications, 12 (1-2): 315–328, doi:10.1016/0898-1221(86)90157-4, MR 838152
- ↑ Janner, Aloysio (June 2001), "DNA enclosing forms from scaled growth forms of snow crystals", Crystal Engineering, 4 (2–3): 119–129, doi:10.1016/S1463-0184(01)00005-3
- ↑ Adams, Arthur G. (1996), The Hudson River Guidebook, Fordham Univ Press, p. 66, ISBN 9780823216796.
- ↑ Bodner, B. Lynn (2009), "The eleven–pointed star polygon design of the Topkapı Scroll", Bridges 2009: Mathematics, Music, Art, Architecture, Culture (PDF), pp. 147–154.
- ↑ Angelo, Joseph A. (2009), Encyclopedia of Space and Astronomy, Infobase Publishing, p. 511, ISBN 9781438110189.